题目内容
现有8名运动员参加110米栏决赛,共有1,2,3,4,5,6,7,8八条跑道,其中甲,乙,丙三名运动员道次各不相邻,丁不在第一道,则安排这8名运动员比赛的方式共有 种.
考点:计数原理的应用
专题:排列组合
分析:利用间接法,先不考虑丁,先排除甲,乙,丙三名运动员的另外5人,然后把甲,乙,丙三名运动员插入到里面即可,再减去丁再第一道的位置的情况,问题得以解决
解答:
解:先不考虑丁,先排除甲,乙,丙三名运动员的另外5人,然后把甲,乙,丙三名运动员所形成的6个间隔中有插入到里面,有
•
=14400种,
若丁在丁在第一道,先排除甲,乙,丙三名运动员的另外4人,然后把甲,乙,丙三名运动员所形成的5个间隔中有插入到里面,有
•
=1440种,
故丁不在第一道,则安排这8名运动员比赛的方式共有14400-1440=12960,
故答案为:12960.
| A | 5 5 |
| A | 3 6 |
若丁在丁在第一道,先排除甲,乙,丙三名运动员的另外4人,然后把甲,乙,丙三名运动员所形成的5个间隔中有插入到里面,有
| A | 4 4 |
| A | 3 5 |
故丁不在第一道,则安排这8名运动员比赛的方式共有14400-1440=12960,
故答案为:12960.
点评:排列与组合问题要区分开,若题目要求元素的顺序则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
已知A、B、C是锐角△ABC的三个内角,向量
=(sinA,1),
=(1,-cosB),则
与
的夹角是( )
| p |
| q |
| p |
| q |
| A、锐角 | B、钝角 | C、直角 | D、不确定 |
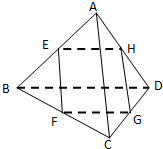 已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,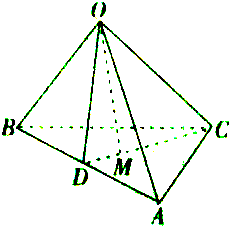 如图所示,点D是AB的中点,点M是△ABC三条中线的交点,O是空间任意一点.求证:
如图所示,点D是AB的中点,点M是△ABC三条中线的交点,O是空间任意一点.求证: