题目内容
设集合I={1，2，3}，A⊆I，若把满足M∪A=I的集合M叫做集合A的配集，则A={1，2}的子集有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：对于有限集合，我们有以下结论：若一个集合中有n个元素，则它有2n个子集．
解答：
解：由定义可知，3∈M，
故集合M有22=4个，
故选D．
故集合M有22=4个，
故选D．
点评：本题考查了集合的子集个数，若一个集合中有n个元素，则它有2n个子集，有（2n-1）个真子集，属于基础题．
练习册系列答案
ABC考王全优卷系列答案
相关题目
已知函数g（x）满足g（x+3）=g（-x），若f（x）在（-2，0）∪（0.2）上为偶函数，且f（x）=
，则g（-2015）=（ ）
|
| A、0 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知向量
=（-1，-2，1），
=（2，x，3），若
⊥（
+
），则实数x的值为（ ）
| a |
| b |
| a |
| a |
| b |
A、-
| ||
| B、3 | ||
C、
| ||
D、
|
已知f（x）=log2x，则f(
)=（ ）
| 1 |
| 2 |
| A、2 | B、1 |
| C、（-1，3） | D、（-1，3） |
设集合M={（x，y）|y=2x2-x-1}，N={y|y=2x2-x-1}，则M∩N（ ）
| A、∅ | B、M | C、N | D、不存在 |
下列说法错误的是（ ）
| A、若命题p：?x∈R，使得x2-x+1=0，则￢p：?x∈R，都有x2-x+1≠0 |
| B、命题“若x2-3x+2=0，则x=1”的否命题为假命题 |
| C、命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0” |
| D、已知p：?x∈R，使得cosx=1，q：?x∈R，都有x2-x+1＞0，则“p∧-q”为假命题 |
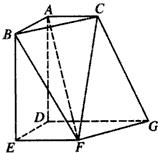如图，在空间中的Rt△ABC与直角梯形EFGD中，平面ABC∥平面DEFG，AD⊥平面DEFG，AC∥DG．且AB=AD=DE=DG=2，AC=EF=1．求二面角D-CG-F的余弦值．设等差数列{an}的前n项和为Sn．若公差d＜0，且|a7|=|a8|，则使Sn＞0的最大正整数n是（ ）
| A、12 | B、13 | C、14 | D、15 |
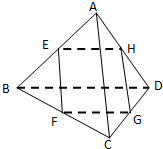已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点，