题目内容
已知O为原点，椭圆
+
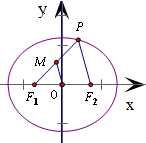
=1上一点P到左焦点F1的距离为4，M是PF1的中点．则|OM|= ．
| x2 |
| 25 |
| y2 |
| 9 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据椭圆的定义，得|PF1|+|PF2|=2a，可得|PF2|=2a-|PF1|=6，在△PF1F2中利用中位线定理，即可得到的|OM|值．
解答：
解：∵椭圆
+
=1中，a=5，
∴|PF1|+|PF2|=2a=10，
结合|PF1|=4，得|PF2|=2a-|PF1|=10-4=6，
∵OM是△PF1F2的中位线，
∴|OM|=
|PF2|=
×6=3．
故答案为：3．
解：∵椭圆| x2 |
| 25 |
| y2 |
| 9 |
∴|PF1|+|PF2|=2a=10，
结合|PF1|=4，得|PF2|=2a-|PF1|=10-4=6，
∵OM是△PF1F2的中位线，
∴|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：3．
点评：本题给出椭圆的焦点三角形的一边长，求另一边中点到原点的距离，着重考查了椭圆的定义和标准方程和简单几何性质等知识，属于中档题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
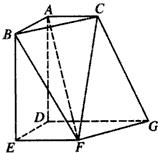如图，在空间中的Rt△ABC与直角梯形EFGD中，平面ABC∥平面DEFG，AD⊥平面DEFG，AC∥DG．且AB=AD=DE=DG=2，AC=EF=1．求二面角D-CG-F的余弦值．
执行如图所示的框图，若输入N=6，则输出的数S等于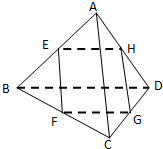
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点，
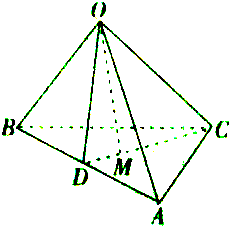如图所示，点D是AB的中点，点M是△ABC三条中线的交点，O是空间任意一点．求证：