题目内容
一双曲线焦点的坐标,离心率分别为(±5,0)、
,则它的共轭双曲线的焦点坐标、离心率分别分别是( )
| 3 |
| 2 |
A、(0,±5),
| ||||||
B、(0,±5),
| ||||||
C、(0,±
| ||||||
D、(0,±
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意求出c=5,
=
,a=
,b=
,从而得到共轭双曲线中的a=
,b=
,c=5,从而求焦点坐标及离心率.
| c |
| a |
| 3 |
| 2 |
| 10 |
| 3 |
5
| ||
| 3 |
5
| ||
| 3 |
| 10 |
| 3 |
解答:
解:由题意可得,c=5,
=
,
∴a=
,b=
,
则它的共轭双曲线中,
a=
,b=
,c=5,
且焦点在y轴,
故共轭双曲线的焦点坐标、离心率分别为
(0,±
),
,
故选A.
| c |
| a |
| 3 |
| 2 |
∴a=
| 10 |
| 3 |
5
| ||
| 3 |
则它的共轭双曲线中,
a=
5
| ||
| 3 |
| 10 |
| 3 |
且焦点在y轴,
故共轭双曲线的焦点坐标、离心率分别为
(0,±
| 5 |
| 3 | ||
|
故选A.
点评:本题考查了双曲线的简单性质,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下列说法错误的是( )
| A、若命题p:?x∈R,使得x2-x+1=0,则¬p:?x∈R,都有x2-x+1≠0 |
| B、命题“若x2-3x+2=0,则x=1”的否命题为假命题 |
| C、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” |
| D、已知p:?x∈R,使得cosx=1,q:?x∈R,都有x2-x+1>0,则“p∧-q”为假命题 |
已知椭圆的一个焦点为F(0,1),离心率e=
,则该椭圆的标准程为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|
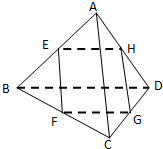 已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,
已知E、F、G、H分别是三棱锥A-BCD 棱AB、BC、CD、DA的中点,