题目内容
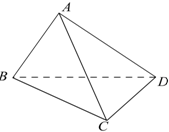 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.(Ⅰ)求证:BC⊥AD;
(Ⅱ)若点D到平面ABC的距离等于3,求二面角A-BC-D的正弦值;
(Ⅲ)设二面角A-BC-D的大小为θ,猜想θ为何值时,四面体A-BCD的体积最大.(不要求证明)
考点:用空间向量求平面间的夹角,棱锥的结构特征,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)取BC中点O,连结AO,DO,由已知得AO⊥BC,DO⊥BC,从而BC⊥平面AOD,由此能证明BC⊥AD.
(2)由(1)知∠AOD为二面角A-BC-D的平面角,由此能求出二面角A-BC-D的正弦值.
(3)由已知条件推导出当 θ=90°时,四面体ABCD的体积最大.
(2)由(1)知∠AOD为二面角A-BC-D的平面角,由此能求出二面角A-BC-D的正弦值.
(3)由已知条件推导出当 θ=90°时,四面体ABCD的体积最大.
解答:
(Ⅰ)证明: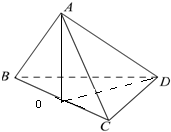 取BC中点O,连结AO,DO,
取BC中点O,连结AO,DO,
∵△ABC与△DBC都是边长为4的正三角形,
∴AO⊥BC,DO⊥BC,
∴BC⊥平面AOD,
∵AD?平面AOD,∴BC⊥AD.
(2)解:由(1)知∠AOD为二面角A-BC-D的平面角,
设∠AOD=θ,则过点D作DE⊥AD,垂足为E.
∵BC⊥平面ADO,且BC?平面ABC,
∴平面ADO⊥平面ABC.又平面ADO∩平面ABC=AO,
∴DE⊥平面ABC.
∴线段DE的长为点D到平面ABC的距离,即DE=3.
又DO=
BD=2
,
在Rt△DEO中,sinθ=
=
,
故二面角A-BC-D的正弦值为
.
(3)当 θ=90°时,四面体ABCD的体积最大.
 取BC中点O,连结AO,DO,
取BC中点O,连结AO,DO,∵△ABC与△DBC都是边长为4的正三角形,
∴AO⊥BC,DO⊥BC,
∴BC⊥平面AOD,
∵AD?平面AOD,∴BC⊥AD.
(2)解:由(1)知∠AOD为二面角A-BC-D的平面角,
设∠AOD=θ,则过点D作DE⊥AD,垂足为E.
∵BC⊥平面ADO,且BC?平面ABC,
∴平面ADO⊥平面ABC.又平面ADO∩平面ABC=AO,
∴DE⊥平面ABC.
∴线段DE的长为点D到平面ABC的距离,即DE=3.
又DO=
| ||
| 2 |
| 3 |
在Rt△DEO中,sinθ=
| DE |
| DO |
| ||
| 2 |
故二面角A-BC-D的正弦值为
| ||
| 2 |
(3)当 θ=90°时,四面体ABCD的体积最大.
点评:本题考查异面直线垂直的证明,考查二面角的正弦值的求法,考查四面体的体积的最大值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
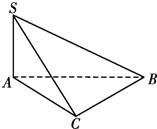 如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2
如图,SA⊥面ABC,∠ACB=90°,∠ABC=30°,AC=1,SB=2