题目内容
已知x，y，z＞0，x+y+z=3，求x2+y2+z2的最小值．
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：构造柯西不等式：（12+12+12）（x2+y2+z2）=3（x2+y2+z2）≥（x+y+z）2这个条件进行计算即可．
解答：
证明：由柯西不等式可得（12+12+12）（x2+y2+z2）≥（x+y+z）2=9，
可得：x2+y2+z2≥3，
即x2+y2+z2的最小值为3，
故答案为：3．
可得：x2+y2+z2≥3，
即x2+y2+z2的最小值为3，
故答案为：3．
点评：本题考查用综合法证明不等式，关键是利用柯西不等式．
练习册系列答案
优学名师名题系列答案
相关题目
如图，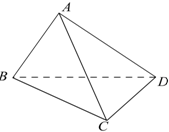
在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．