题目内容
已知下列不等式①x2-4x+3＜0；②x2-6x+8＜0；③2x2-9x+a＜0．要使①②成立的x也满足③，请你找一个这样的a值．
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：联立①②，解得2＜x＜3．由于2＜x＜3也满足③2x2-9x+a＜0，可得③的解集非空且（2，3）是③解集的子集，即可得到a的范围，从而得到答案．
解答：
解：联立①②得
，即
，解得2＜x＜3．
∵2＜x＜3也满足③2x2-9x+a＜0，
∴③的解集非空且（2，3）是③解集的子集．
由f（x）=2x2-9x+a＜0，
∴f（2）=8-18+a≤0，且f（3）=18-27+a≤0，解得a≤9．
∴a的范围是（-∞，9]，
这样a的值可取小于等于9中的任一个，不妨取9．
故答案为：9（不唯一）
|
|
∵2＜x＜3也满足③2x2-9x+a＜0，
∴③的解集非空且（2，3）是③解集的子集．
由f（x）=2x2-9x+a＜0，
∴f（2）=8-18+a≤0，且f（3）=18-27+a≤0，解得a≤9．
∴a的范围是（-∞，9]，
这样a的值可取小于等于9中的任一个，不妨取9．
故答案为：9（不唯一）
点评：本题考查了不等式组的解法、集合之间的关系，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
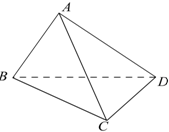在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．