题目内容
已知函数y=2sin(
-4x).
(Ⅰ)求函数的周期及单调区间;
(Ⅱ)求函数的最大值及最小值并写出取最值时自变量x的集合.
| π |
| 3 |
(Ⅰ)求函数的周期及单调区间;
(Ⅱ)求函数的最大值及最小值并写出取最值时自变量x的集合.
考点:三角函数的最值,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(Ⅰ)利用诱导公式化数y=2sin(
-4x)为y=-2sin(4x-
),然后直接利用周期公式求周期,由复合函数的单调性求单调区间;
(Ⅱ)由(Ⅰ)中求得的单调区间直接得到函数的最值及取得最值时的x的集合.
| π |
| 3 |
| π |
| 3 |
(Ⅱ)由(Ⅰ)中求得的单调区间直接得到函数的最值及取得最值时的x的集合.
解答:
(Ⅰ)函数y=2sin(
-4x)=-2sin(4x-
)
则周期T=
=
.
2sin(4x-
)的单调递增区间即原函数的单调递减区间.
由-
+2kπ≤4x-
≤
+2kπ,
解得原函数的单调递减区间为[-
+
,
+
]k∈Z.
由
+2kπ≤4x-
≤
π+2kπ,
解得原函数的单调递增区间为[
+
,
+
]k∈Z;
(Ⅱ)由于函数在[-
+
,
+
]k∈Z单调递减,
∴当x∈{x|x=-
+
,k∈Z}时函数取得最大值为2.
当x∈{x|x=
+
,k∈Z}时函数取得最小值为-2.
| π |
| 3 |
| π |
| 3 |
则周期T=
| 2π |
| 4 |
| π |
| 2 |
2sin(4x-
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得原函数的单调递减区间为[-
| π |
| 24 |
| kπ |
| 2 |
| 5π |
| 24 |
| kπ |
| 2 |
由
| π |
| 2 |
| π |
| 3 |
| 3 |
| 2 |
解得原函数的单调递增区间为[
| 5π |
| 24 |
| kπ |
| 2 |
| 11π |
| 24 |
| kπ |
| 2 |
(Ⅱ)由于函数在[-
| π |
| 24 |
| kπ |
| 2 |
| 5π |
| 24 |
| kπ |
| 2 |
∴当x∈{x|x=-
| π |
| 24 |
| kπ |
| 2 |
当x∈{x|x=
| 5π |
| 24 |
| kπ |
| 2 |
点评:本题考查了三角函数的周期性及求法,考查了与三角函数有关的符合函数的单调性,考查了三角函数的最值,是基础题.

练习册系列答案
相关题目
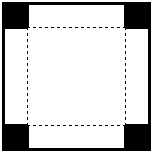 如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
如图,一边长为48cm的正方形铁皮,在它的四角上切去相等的小正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?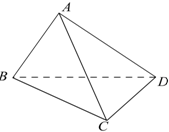 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.