题目内容
已知在等差数列{an}中,若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq.类比上述性质,在等比数列{an}中,则有 .
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:结合等差数列与等比数列具有类比性,且等差数列与和差有关,等比数列与积商有关,因此等比数列类比到等差数列的:若m+n=p+q(m,n,p,q∈N*),则am•an=ap•aq.
解答:
解:类比上述性质,在等比数列{an}中,则有若m+n=p+q(m,n,p,q∈N*),则am•an=ap•aq,
故答案为:若m+n=p+q(m,n,p,q∈N*),则am•an=ap•aq.
故答案为:若m+n=p+q(m,n,p,q∈N*),则am•an=ap•aq.
点评:本题主要考查等差数列类比到等比数列的类比推理,类比推理一般步骤:①找出等差数列、等比数列之间的相似性或者一致性.②用等差数列的性质去推测物等比数列的性质,得出一个明确的命题(或猜想).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
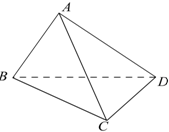 在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.
在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.