题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程为2x+y=0,且顶点到渐近线的距离为
.
(1)求此双曲线的方程;
(2)设点P为双曲线上一点,A、B两点在双曲线的渐近线上,且分别位于第一、第二象限,若
=
,求△AOP的面积.
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 5 |
(1)求此双曲线的方程;
(2)设点P为双曲线上一点,A、B两点在双曲线的渐近线上,且分别位于第一、第二象限,若
| AP |
| PB |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用双曲线渐近线方程为2x+y=0,且顶点到渐近线的距离为
,求出a,b,即可求此双曲线的方程;
(2)由A(m,2m),B(-n,2n),根据
=
,得P点的坐标代入双曲线方程化简整理m,n的关系式;设∠AOB=2θ,进而根据直线的斜率求得tanθ,进而求得sin2θ,进而表示出|OA|,得到△AOB的面积的表达式,即可得出结论.
2
| ||
| 5 |
(2)由A(m,2m),B(-n,2n),根据
| AP |
| PB |
解答:
解:(1)∵一条渐近线方程为2x+y=0,且顶点到渐近线的距离为
,
∴
=
,
∴a=1,
∵
=2,
∴b=2,
∴双曲线的方程为x2-
=1;
(2)由(1)知双曲线C的两条渐近线方程为y=±2x.
设A(m,2m),B(-n,2n),m>0,n>0.
∵
=
,
∴P(
,m+n),
代入x2-
=1化简得,mn=1,
设∠AOB=2θ,则tanθ=2,所以sin2θ=
,
又|OA|=
m,|OB|=
n,
所以S△AOB=
|OA||OB|sin2θ=2mn=2.
2
| ||
| 5 |
∴
| |2a| | ||
|
2
| ||
| 5 |
∴a=1,
∵
| b |
| a |
∴b=2,
∴双曲线的方程为x2-
| y2 |
| 4 |
(2)由(1)知双曲线C的两条渐近线方程为y=±2x.
设A(m,2m),B(-n,2n),m>0,n>0.
∵
| AP |
| PB |
∴P(
| m-n |
| 2 |
代入x2-
| y2 |
| 4 |
设∠AOB=2θ,则tanθ=2,所以sin2θ=
| 4 |
| 5 |
又|OA|=
| 5 |
| 5 |
所以S△AOB=
| 1 |
| 2 |
点评:本题主要考查了双曲线的标准方程和直线与圆锥曲线的综合问题.考查了学生综合分析问题的能力,属于中档题.

练习册系列答案
相关题目
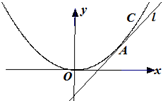 如图,直线l:y=x+b与曲线C:x2=4y相切于点A.
如图,直线l:y=x+b与曲线C:x2=4y相切于点A.