题目内容
2.已知A(-1,1),B(3,1),C(1,3),则△ABC的BC边上的高所在的直线的方程为( )| A. | x+y+2=0 | B. | x+y=0 | C. | x-y+2=0 | D. | x-y=0 |
分析 根据垂直关系求出高线的斜率,利用点斜式方程求出.
解答 解:边BC所在直线的斜率kBC=$\frac{3-1}{1-3}$=-1,∴BC边上的高线斜率k=1.
又∵BC边上的高线经过点A(-1,1),
∴BC边上的高线方程为y-1=x+1,即x-y+2=0.
故选C.
点评 本题考查了直线方程的求法,属于基础题.

练习册系列答案
相关题目
17.在数列{an}中,对任意的n∈N*,都有an-an+1=10,则数列{an}是( )
| A. | 递增数列 | B. | 递减数列 | C. | 常数列 | D. | 摆动数列 |
7.命题“?x∈R,sinx+cosx≤$\sqrt{2}$”的否定是( )
| A. | ?x∈R,sinx+cosx>$\sqrt{2}$ | B. | ?x∈R,sinx+cosx≤$\sqrt{2}$ | ||
| C. | ?x∈R,sinx+cosx≥$\sqrt{2}$ | D. | ?x∈R,sinx+cosx>$\sqrt{2}$ |
14.已知集合A={1,2,3},B={x|(x-3)(x-6)=0},则A∩B等于( )
| A. | {1} | B. | {2,3} | C. | {3,6} | D. | {3} |
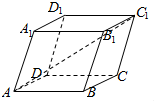 已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.
已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.