题目内容
20.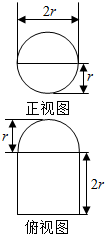 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为4+5π,则半径r=1.
分析 通过三视图可知该几何体是一个半球和半个圆柱所成的组合体,根据几何体的表面积,构造关于r的方程,计算即可得到答案.
解答  解:由几何体三视图中的正视图和俯视图可知,
解:由几何体三视图中的正视图和俯视图可知,
截圆柱的平面过圆柱的轴线,
该几何体是一个半球拼接半个圆柱,
∴其表面积为:$\frac{1}{2}$×4πr2+$\frac{1}{2}$×πr2+$\frac{1}{2}$×2r×2πr+2r×2r+$\frac{1}{2}$×πr2=5πr2+4r2,
又∵该几何体的表面积为4+5π,
∴5πr2+4r2=4+5π,解得r=1,
故答案为:1
点评 本题考查由三视图求表面积问题,考查空间想象能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
8.已知命题p:“?x∈R,x+1≥0”的否定是“?x∈R,x+1<0”;命题q:函数y=x-3是幂函数,则下列命题为真命题的是( )
| A. | p且q | B. | p或q | C. | ¬q | D. | p且(¬q) |
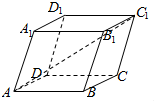 已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$.
已知平行六面体ABCD-A1B1C1D1所有棱长均为1,∠BAD=∠BAA1=∠DAA1=60°,则AC1的长为$\sqrt{6}$. 如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.
如图长方体ABCD-A1B1C1D1中,AB=AA1=1,BC=$\sqrt{2}$,M是AD的中点,N是B1C1中点.