题目内容
8.一个袋中装有6个红球和4个白球(这10个球各不相同),不放回地依次摸出2个球,在第一次摸出红球的条件下,第二次摸出红球的概率为$\frac{5}{9}$.分析 首先第一次摸出红球为事件A,第二次摸出红球为事件B,分别求出P(A),P(AB),利用条件概率公式求值.
解答 解:设第一次摸出红球为事件A,第二次摸出红球为事件B,
则P(A)=$\frac{{C}_{6}^{1}}{{C}_{10}^{1}}=\frac{3}{5}$,P(AB)=$\frac{{C}_{6}^{2}}{{C}_{10}^{2}}=\frac{15}{45}=\frac{1}{3}$.
∴P(B|A)=$\frac{P(AB)}{P(A)}=\frac{5}{9}$.
故答案为:$\frac{5}{9}$
点评 本题考查了条件概率的求法;利用条件概率公式,只要分别求出第一次摸出红球为事件A的概率,以及第二次摸出红球为事件B,P(AB),利用条件概率公式解答.

练习册系列答案
相关题目
3.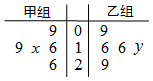 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
17.数列{an}满足a1=2,a2=1,并且$\frac{{a}_{n}}{{a}_{n-1}}$+$\frac{{a}_{n}}{{a}_{n+1}}$=2(n≥2),则数列{an}的第100项为( )
| A. | $\frac{1}{{{2^{100}}}}$ | B. | $\frac{1}{{{2^{50}}}}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{50}$ |
18.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{5}$ |