题目内容
已知定义在R的函数f(x),其导函数f′(x)的部分图象如图所示,则下列判断一定正确的是( )
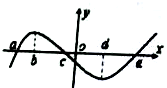

| A、f(a)=f(c)=f(e) |
| B、f(b)>f(c)>f(d) |
| C、f(c)>f(b)>f(a) |
| D、f(c)>f(d)>f(a) |
考点:函数的图象
专题:函数的性质及应用
分析:从导函数的图象得出导数的正负以及原函数的单调区间,画出y=f(x)的大致图象,再选择答案.
解答:
解:从导函数f′(x)的部分图象上看,
当x∈(a,c)时,f′(x)>0,∴f(x)在(a,c)上单调递增;
当x∈(c,e)时,f′(x)<0,∴f(x)在(c,e)上单调递减;
当x<a时,f′(x)<0,∴f(x)在x<a单调递减;
当x>e时,f′(x)>0,∴f(x)在x>e单调递增;
而当x=a时函数取极小值,当x=c时函数取极大值,当x=e时函数取极小值,
∴y=f(x)的图象大致为:
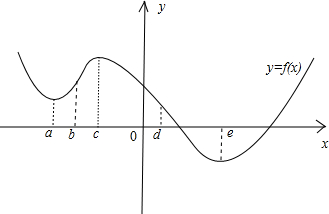
从图象上看,f(c)>f(b)>f(a),
故选:C.
当x∈(a,c)时,f′(x)>0,∴f(x)在(a,c)上单调递增;
当x∈(c,e)时,f′(x)<0,∴f(x)在(c,e)上单调递减;
当x<a时,f′(x)<0,∴f(x)在x<a单调递减;
当x>e时,f′(x)>0,∴f(x)在x>e单调递增;
而当x=a时函数取极小值,当x=c时函数取极大值,当x=e时函数取极小值,
∴y=f(x)的图象大致为:

从图象上看,f(c)>f(b)>f(a),
故选:C.
点评:本题主要考查函数的单调性、极值与函数的导数之间的关系,特别地,由导函数的图象可画出原函数的大致图象,对于研究函数来说,是一个行之有效的方法.

练习册系列答案
相关题目
已知A={y|y=-x2+1,x∈R},B=N,则A∩B是( )
| A、{1} | B、{0,1} |
| C、{(0,1)} | D、R |
已知四个函数:①y=f1(x)②y=f2(x)③y=f3(x)④y=f4(x)的图象分别如图所示,则下列等式成立的是( )
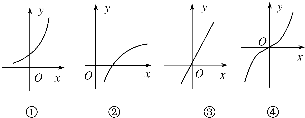

| A、f1(x1+x2)=f1(x1)+f1(x2) |
| B、f2(x1+x2)=f2(x1)+f2(x2) |
| C、f3(x1+x2)=f3(x1)+f3(x2) |
| D、f4(x1+x2)=f4(x1)+f4(x2) |