题目内容
已知A={y|y=-x2+1，x∈R}，B=N，则A∩B是（ ）
| A、{1} | B、{0，1} |
| C、{（0，1）} | D、R |
考点：交集及其运算
专题：集合
分析：根据题意，求出集合A中函数y=-x2+1的值域即可得到A集合，再求出两集合的交集即可．
解答：
解：∵y=-x2+1≤1，
∴集合A=（-∞，1]，
又B=N
则A∩B={y|y=0或y=1}
故选：B．
∴集合A=（-∞，1]，
又B=N
则A∩B={y|y=0或y=1}
故选：B．
点评：此题属于以函数的值域为平台，考查了求交集的运算，是一道基础题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
已知
=（-2，3），
=（x，-6），且
∥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、4 | B、-4 | C、9 | D、-9 |
定义在集合{1，2，3，4}上的函数f（x），g（x）分别由下表给出：
则与f[g（1）]相同的是（ ）
| x | 1 | 2 | 3 | 4 | x | 1 | 2 | 3 | 4 | |
| f（x） | 3 | 4 | 2 | 1 | g（x） | 4 | 3 | 1 | 2 |
| A、g（f（3）） |
| B、g（f（1）） |
| C、g（f（4）） |
| D、g（f（2）） |
复数z满足（1+i）z=i（i为虚数单位），则在复平面上，复数z对应的点在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知定义在R的函数f（x），其导函数f′（x）的部分图象如图所示，则下列判断一定正确的是（ ）
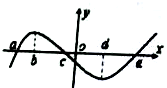
| A、f（a）=f（c）=f（e） |
| B、f（b）＞f（c）＞f（d） |
| C、f（c）＞f（b）＞f（a） |
| D、f（c）＞f（d）＞f（a） |
