题目内容
甲乙等5人排队，要求甲乙必须站在一起的站法共有 种．
考点：计数原理的应用
专题：计算题,概率与统计
分析：根据题意，用捆绑法分析，首先把甲和乙看做一个元素，使得它与另外4个元素排列，再者甲和乙之间还有一个排列，根据分步计数原理得到结果．
解答：
解：根据题意，5人排成一排，其中甲、乙两人必须排在一起，
首先把甲和乙看做一个元素，考虑甲乙的位置有2种情况，
再将甲乙这个元素与另外4个元素排列，有A44=24种顺序，
则共有2×24=48种不同的站法；
故答案为：48．
首先把甲和乙看做一个元素，考虑甲乙的位置有2种情况，
再将甲乙这个元素与另外4个元素排列，有A44=24种顺序，
则共有2×24=48种不同的站法；
故答案为：48．
点评：本题考查排列、组合及简单计数问题，考查相邻问题，利用捆绑法分析即可．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知
=（-2，3），
=（x，-6），且
∥
，则实数x的值为（ ）
| a |
| b |
| a |
| b |
| A、4 | B、-4 | C、9 | D、-9 |
设函数f（x）和g（x）分别是R上的偶函数和奇函数，则下列结论成立的是（ ）
| A、f（x）+g（x）是偶函数 |
| B、f（x）•g（x）是偶函数 |
| C、f（x）+g（x）是奇函数 |
| D、f（x）•g（x）是奇函数 |
-685°的终边落在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
定义在集合{1，2，3，4}上的函数f（x），g（x）分别由下表给出：
则与f[g（1）]相同的是（ ）
| x | 1 | 2 | 3 | 4 | x | 1 | 2 | 3 | 4 | |
| f（x） | 3 | 4 | 2 | 1 | g（x） | 4 | 3 | 1 | 2 |
| A、g（f（3）） |
| B、g（f（1）） |
| C、g（f（4）） |
| D、g（f（2）） |
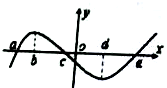
已知定义在R的函数f（x），其导函数f′（x）的部分图象如图所示，则下列判断一定正确的是（ ）
| A、f（a）=f（c）=f（e） |
| B、f（b）＞f（c）＞f（d） |
| C、f（c）＞f（b）＞f（a） |
| D、f（c）＞f（d）＞f（a） |