题目内容
已知函数f（x）
，则方程f（2x2+x）=a（a＞2）的根的个数可能为 （将正确命题的序号全部填入）
①1个 ②2个 ③3个 ④4个 ⑤5 个 ⑥6个．
|
①1个 ②2个 ③3个 ④4个 ⑤5 个 ⑥6个．
考点：根的存在性及根的个数判断
专题：作图题,函数的性质及应用
分析：先画出函数f（x）=
的图象，然后令t=2x2+x，讨论a的范围，得到y=a与y=f（t）的图象交点的个数，再结合交点的值讨论t=2x2+x的解得个数，即可求出方程f（2x2+x）=a（a＞2）的根的个数可能．
|
解答：
解：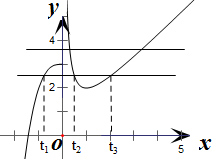
画出函数f（x）=
的图象如右图，
令t=2x2+x，
当2＜a≤3时，y=a与y=f（t）的图象有三个交点，三个交点的横坐标记为t1，t2，t3且t1≤0＜t2＜t3，
当2x2+x=t2时，该方程有两解，2x2+x=t3时，该方程也有两解，2x2+x=t1时，该方程有0个解或1个解或2个解，
∴当2＜a≤3时，方程f（2x2+x）=a的根的个数可能为4个，5个，6个；
当a＞3时，y=a与y=f（t）的图象有两个交点，两个交点的横坐标记为t4，t5且0＜t4＜t5，
当2x2+x=t4时，该方程有两解，2x2+x=t5时，该方程也有两解，
∴当a＞3时，方程f（2x2+x）=a的根的个数为4个；
综上所述：方程f（2x2+x）=a（a＞2）的根的个数可能为4个，5个，6个．
故答案为：④⑤⑥．
画出函数f（x）=
|
令t=2x2+x，
当2＜a≤3时，y=a与y=f（t）的图象有三个交点，三个交点的横坐标记为t1，t2，t3且t1≤0＜t2＜t3，
当2x2+x=t2时，该方程有两解，2x2+x=t3时，该方程也有两解，2x2+x=t1时，该方程有0个解或1个解或2个解，
∴当2＜a≤3时，方程f（2x2+x）=a的根的个数可能为4个，5个，6个；
当a＞3时，y=a与y=f（t）的图象有两个交点，两个交点的横坐标记为t4，t5且0＜t4＜t5，
当2x2+x=t4时，该方程有两解，2x2+x=t5时，该方程也有两解，
∴当a＞3时，方程f（2x2+x）=a的根的个数为4个；
综上所述：方程f（2x2+x）=a（a＞2）的根的个数可能为4个，5个，6个．
故答案为：④⑤⑥．
点评：本题考查了根的存在性及根的个数的判断，以及符号函数的性质，同时考查了作图的能力，分析问题的能力和转化的思想以及分类讨论的思想．属于中档题．
练习册系列答案
相关题目
直线kx-y=k+2和x-ky=k（k＞1）与y轴围成的三角形的面积的最小值为（ ）
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|