题目内容
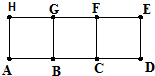 已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.
已知长方形ADEH是由三个边长为1的正方形拼接而成的,从ABCDEFGH这八个点中任取三个点组成的图形面积记为ξ,当三点共线时ξ=0.(1)求ξ=0时的概率;
(2)求ξ的分布列和Eξ.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式
专题:概率与统计
分析:(1)利用古典概率的计算公式能求出ξ=0时的概率.
(2)由题意知ξ=0,
,1,
,分别求出相对应的概率,由此能求出ξ的分布列和Eξ.
(2)由题意知ξ=0,
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)ξ=0时,
P(ξ=0)=
=
=
…(4分)
(2)由题意知ξ=0,
,1,
…(6分)
P(ξ=0)=
,
P(ξ=
)=
,
P(ξ=1)=
,
P(ξ=
)=
,…(10分)
∴ξ的分布列为:
∴E(ξ)=0×
+
•
+1•
+
•
=
=
=
.…(13分)
P(ξ=0)=
| ||||
|
| 8 |
| 56 |
| 1 |
| 7 |
(2)由题意知ξ=0,
| 1 |
| 2 |
| 3 |
| 2 |
P(ξ=0)=
| 8 |
| 56 |
P(ξ=
| 1 |
| 2 |
| 24 |
| 56 |
P(ξ=1)=
| 16 |
| 56 |
P(ξ=
| 3 |
| 2 |
| 8 |
| 56 |
∴ξ的分布列为:
| ξ | 0 |
|
1 |
| ||||||||
| P |
|
|
|
|
| 8 |
| 56 |
| 1 |
| 2 |
| 24 |
| 56 |
| 16 |
| 56 |
| 3 |
| 2 |
| 8 |
| 56 |
| 12+16+12 |
| 56 |
| 40 |
| 56 |
| 5 |
| 7 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设Sn是等差数列{an}的前n项和,若
=1,则
=( )
| S11 |
| S9 |
| a6 |
| a5 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、
|
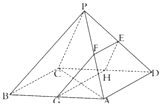 如图,四棱锥P-ABCD中,底面ABCD是边长为2
如图,四棱锥P-ABCD中,底面ABCD是边长为2