题目内容
已知α,β均为锐角,且sinα=
,sin(α-β)=-
.
(1)求tan(α-β)的值;
(2)求cosβ的值.
| 3 |
| 5 |
| ||
| 10 |
(1)求tan(α-β)的值;
(2)求cosβ的值.
考点:两角和与差的正切函数,两角和与差的正弦函数
专题:计算题,三角函数的求值
分析:(1)确定-
<α-β<0,求出cos(α-β)=
,即可求tan(α-β)的值;
(2)利用cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β),即可求cosβ的值.
| π |
| 2 |
3
| ||
| 10 |
(2)利用cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β),即可求cosβ的值.
解答:
解:(1)∵α,β∈(0,
),∴-
<α-β<
.…(2分)
又sin(α-β)=-
,∴-
<α-β<0…(4分)
∴cos(α-β)=
,∴tan(α-β)=-
…(7分)
(2)∵α为锐角,sinα=
,∴cosα=
. …(8分)
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
×
+
×(-
)=
. …(14分)
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
又sin(α-β)=-
| ||
| 10 |
| π |
| 2 |
∴cos(α-β)=
3
| ||
| 10 |
| 1 |
| 3 |
(2)∵α为锐角,sinα=
| 3 |
| 5 |
| 4 |
| 5 |
∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)…(12分)
=
| 4 |
| 5 |
3
| ||
| 10 |
| 3 |
| 5 |
| ||
| 10 |
9
| ||
| 50 |
点评:本题考查两角和与差的三角函数,考查角的变换,正确运用公式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知△ABC中,A,B,C的对边分别为a,b,c,且
已知△ABC中,A,B,C的对边分别为a,b,c,且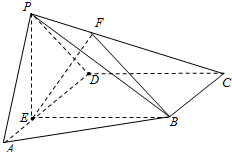 如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.
如图,在四棱锥P-ABCD中,E为AD上一点,PE⊥平面ABCD.AD∥BC,AD⊥CD,BC=ED=2AE=2,EB=3,F为PC上一点,且CF=2FP.