题目内容
在平面直角坐标系xOy中,点A(0,3),直线l经过两点(1,-2),(3,2),设圆C的半径为1,圆心在直线l上.
(Ⅰ)求直线l的方程;
(Ⅱ)若圆C被x轴截得的弦长为
,求圆C的方程;
(Ⅲ)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
(Ⅰ)求直线l的方程;
(Ⅱ)若圆C被x轴截得的弦长为
| 3 |
(Ⅲ)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
考点:直线和圆的方程的应用
专题:直线与圆
分析:(Ⅰ)求出直线的斜率,利用点斜式方程即可求直线l的方程;
(Ⅱ)若根据直线和圆的位置关系即可求圆C的方程;
(Ⅲ)根据条件MA=2MO,建立条件关系即可得到结论.
(Ⅱ)若根据直线和圆的位置关系即可求圆C的方程;
(Ⅲ)根据条件MA=2MO,建立条件关系即可得到结论.
解答:
解:(Ⅰ)由已知,直线l的斜率k=
=
,
∴直线l的方程为y-2=
(x-3),即2x-y-4=0.
(Ⅱ)∵圆C的圆心在直线l上,可设圆心坐标为(a,2a-4),
由已知可得:|2a-4|=
,
∴a=
或a=
,
∴圆C方程为:(x-
)2+(y-
)2=1,或(x-
)2+(y+
)2=1.
(Ⅲ)∵圆C的圆心在在直线l:y=2x-4上,
∴设圆心C为(a,2a-4)
则圆C的方程为:(x-a)2+[y-(2a-4)]2=1,
又∵MA=2MO,
∴设M为(x,y)则
=2
整理得:x2+(y+1)2=4设为圆D,
∴点M应该既在圆C上又在圆D上
即:圆C和圆D有交点
∴|2-1|≤
≤|2+1|,
由5a2-8a+8≥0得x∈R
由5a2-12a≤0得0≤x≤
终上所述,a的取值范围为:[0,
].
| 2+2 |
| 3-1 |
| 1 |
| 2 |
∴直线l的方程为y-2=
| 1 |
| 2 |
(Ⅱ)∵圆C的圆心在直线l上,可设圆心坐标为(a,2a-4),
由已知可得:|2a-4|=
| 1 |
| 2 |
∴a=
| 9 |
| 4 |
| 7 |
| 4 |
∴圆C方程为:(x-
| 9 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 1 |
| 2 |
(Ⅲ)∵圆C的圆心在在直线l:y=2x-4上,
∴设圆心C为(a,2a-4)
则圆C的方程为:(x-a)2+[y-(2a-4)]2=1,
又∵MA=2MO,
∴设M为(x,y)则
| x2+(y-3)2 |
| x2+y2 |
∴点M应该既在圆C上又在圆D上
即:圆C和圆D有交点
∴|2-1|≤
| a2+[(2a-4)-(-1)]2 |
由5a2-8a+8≥0得x∈R
由5a2-12a≤0得0≤x≤
| 12 |
| 5 |
终上所述,a的取值范围为:[0,
| 12 |
| 5 |
点评:本题主要考查直线方程的求法,直线和圆的位置关系的应用,要求熟练掌握相应的方程,考查学生的计算能力.

练习册系列答案
相关题目
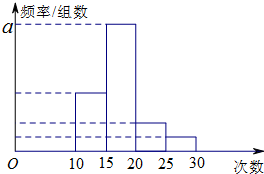 对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下:
对某校高三学生一个月内参加体育活动的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加体育活动的次数.根据此数据做出了频数与频率的统计表和频率分布直方图如下: