题目内容
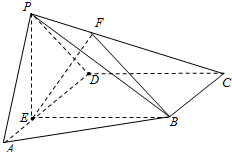如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD．AD∥BC，AD⊥CD，BC=ED=2AE=2，EB=3，F为PC上一点，且CF=2FP．（Ⅰ）求证：PA∥平面BEF；
（Ⅱ）若二面角F-BE-C为60°，求tan∠APD的值．
考点：与二面角有关的立体几何综合题,直线与平面平行的判定
专题：空间角
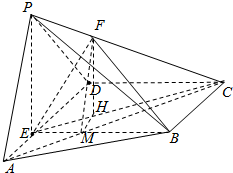
分析：（Ⅰ） 连接AC交BE于点M，连接FM．由EM∥CD，推导出FM∥AP，由此能证明PA∥面BEF．
（Ⅱ）法一：连CE，过F作FH⊥CE于H，过H作HM⊥BE于M，连FM，由已知条件推导出∠FMH为二面角F-BE-C的平面角，由此能求出tan∠APD的值．
（Ⅱ）法二：以E为坐标原点，EB，ED，EP为x，y，z轴建立空间直角坐标系．利用向量法能求出能求出tan∠APD的值．
（Ⅱ）法一：连CE，过F作FH⊥CE于H，过H作HM⊥BE于M，连FM，由已知条件推导出∠FMH为二面角F-BE-C的平面角，由此能求出tan∠APD的值．
（Ⅱ）法二：以E为坐标原点，EB，ED，EP为x，y，z轴建立空间直角坐标系．利用向量法能求出能求出tan∠APD的值．
解答：
（本小题满分15分）
（Ⅰ） 证明：连接AC交BE于点M，
连接FM．∵EM∥CD，
∴
=
=
=
，FM∥AP，
∵FM?面BEF，PA?面BEF，
∴PA∥面BEF．（6分）
（Ⅱ）解法一：连CE，过F作FH⊥CE于H．由于FH∥PE，
∴FH⊥面ABCD．过H作HM⊥BE于M，
连FM．则FM⊥BE，即∠FMH为二面角F-BE-C的平面角．
∴∠FMH=60°，FH=
MH，（10分）
FH=
PE，MH=
BC=
AE，∴PE=
AE，（12分）
tan∠APE=
，tan∠DPE=
，tan∠APD=3
．（15分）
（Ⅱ）解法二：以E为坐标原点，EB，ED，EP为x，y，z轴，
建立空间直角坐标系．
则E（0，0，0），B（3，0，0），P（0，0，m），
C（3，2，0），∵
=2
，∴F(1，
，
m)，（8分）
设平面BEF的法向量
=(x，y，z)，
由
，得
=（0，-m，1），
面ABCD法向量为
=(0，0，1)．（10分）
由于cos60°=
，解得m=
．（12分）
∴tan∠APE=
，tan∠DPE=
，tan∠APD=3
．（15分）
（本小题满分15分）（Ⅰ） 证明：连接AC交BE于点M，
连接FM．∵EM∥CD，
∴
| AM |
| MC |
| AE |
| ED |
| 1 |
| 2 |
| PF |
| FC |
∵FM?面BEF，PA?面BEF，
∴PA∥面BEF．（6分）
（Ⅱ）解法一：连CE，过F作FH⊥CE于H．由于FH∥PE，
∴FH⊥面ABCD．过H作HM⊥BE于M，
连FM．则FM⊥BE，即∠FMH为二面角F-BE-C的平面角．
∴∠FMH=60°，FH=
| 3 |
FH=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
tan∠APE=
| 1 | ||
|
| 2 | ||
|
| 3 |
（Ⅱ）解法二：以E为坐标原点，EB，ED，EP为x，y，z轴，
建立空间直角坐标系．
则E（0，0，0），B（3，0，0），P（0，0，m），
C（3，2，0），∵
| CF |
| FP |
| 2 |
| 3 |
| 2 |
| 3 |
设平面BEF的法向量
| n1 |
由
|
| n1 |
面ABCD法向量为
| n2 |
由于cos60°=
| ||||
|
|
| 3 |
∴tan∠APE=
| 1 | ||
|
| 2 | ||
|
| 3 |
点评：本题考查直线与平面平行的证明，考查角的正切值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
