题目内容
 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=| 2 |
(1)证明:AD⊥CE;
(2)求二面角A-CE-B的正切值.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:空间角
分析:(1)根据线面垂直的性质,即可证明:AD⊥CE;
(2)求出二面角的平面角,即可求二面角A-CE-B的正切值.
(2)求出二面角的平面角,即可求二面角A-CE-B的正切值.
解答:
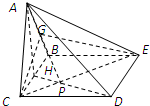 证明:(1)如图,取BC的中点H,连接HD交CE于点P,
证明:(1)如图,取BC的中点H,连接HD交CE于点P,
连接 AH、AP.
∵AB=AC,
∴AH⊥BC
又∵平面ABC⊥平面BCDE,
∴AH⊥平面BCDE,
∴AH⊥CE,
又∵
=
=
,
∴Rt△HCD∽Rt△CDE
∴∠CDH=∠CED,
∴HD⊥CE
∴CE⊥平面AHD
∴AD⊥CE.
(2)由(1)CE⊥平面AHD,∴AP⊥CE,
又HD⊥CE
∴∠APH就是二面角A-CE-B 的平面角,
过点C作CG⊥AB,垂足为G,连接CG、EG.
∵BE⊥BC,且BE⊥AH,
∴BE⊥平面ABC,
∴BE⊥CG,
∴CG⊥平面ABE,
∴∠CEG就是CE与平面ABE所成的角,即∠CEG=45°,
又CE=
,∴CG=EG=
.
又BC=2,∴∠ABC=60°,
∴AB=BC=AC=2,
∴AH=
又HD=
,∴HP=
=
,
∴tan∠APH=
=3.
 证明:(1)如图,取BC的中点H,连接HD交CE于点P,
证明:(1)如图,取BC的中点H,连接HD交CE于点P,连接 AH、AP.
∵AB=AC,
∴AH⊥BC
又∵平面ABC⊥平面BCDE,
∴AH⊥平面BCDE,
∴AH⊥CE,
又∵
| HC |
| CD |
| CD |
| DE |
| 1 | ||
|
∴Rt△HCD∽Rt△CDE
∴∠CDH=∠CED,
∴HD⊥CE
∴CE⊥平面AHD
∴AD⊥CE.
(2)由(1)CE⊥平面AHD,∴AP⊥CE,
又HD⊥CE
∴∠APH就是二面角A-CE-B 的平面角,
过点C作CG⊥AB,垂足为G,连接CG、EG.
∵BE⊥BC,且BE⊥AH,
∴BE⊥平面ABC,
∴BE⊥CG,
∴CG⊥平面ABE,
∴∠CEG就是CE与平面ABE所成的角,即∠CEG=45°,
又CE=
| 6 |
| 3 |
又BC=2,∴∠ABC=60°,
∴AB=BC=AC=2,
∴AH=
| 3 |
又HD=
| 3 |
| CH2 |
| HD |
| ||
| 3 |
∴tan∠APH=
| AH |
| HP |
点评:本题主要考查空间直线垂直的证明,以及二面角大小的求解,考查学生的运算推理能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设奇函数f(x)定义在(-∞,0)∪(0,+∞)上,f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式
<0的解集为( )
| 3f(x)-2f(-x) |
| 5x |
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |
给出下列命题:
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
)x在(0,+∞)上恰有两个零点x1,x2且x1•x2<1.
其中正确命题的个数是( )
①函数y=2-|x|为偶函数;
②函数y=1是周期函数;
③函数f(x)=2x-x2的零点有2个;
④函数g(x)=|log2x|-(
| 1 |
| 2 |
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
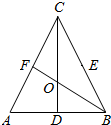 在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量
在△ABC中,D、E、F分别是AB、BC、CA的中点,BF与CD交于点O,设向量