题目内容
7．已知命题p：?c＞0，y=（5-c）x在R上是增函数，命题q：?x∈R，x2+2x+c＞0，若p∧q为假命题，p∨q为真命题，求实数c的取值范围．分析 先求出命题p、q为真时m的范围，由p、q一真一假列式求解
解答 解：命题p真：?c＞0，y=（5-c）x在R上是增函数，∴0＜c＜4，
命题q真：?x∈R，x2+2x+c＞0⇒△=4-4c＜0⇒c＞1；
若p∧q为假命题，p∨q为真命题，则p、q一真一假，
①p为真q为假时，$\left\{\begin{array}{l}{0＜c＜4}\\{c≤1}\end{array}\right.$⇒0＜c≤1；
②p为假q为真时，$\left\{\begin{array}{l}{c≤0\\;或c≥4}\\{c＞1}\end{array}\right.$⇒c≥4；
综上实数c的取值范围为：（0，1]∪[4，+∞）
点评 本题考查了命题真假的应用，属于基础题．
练习册系列答案
相关题目
9．已知x≥5，则f（x）=$\frac{{x}^{2}-4x+9}{x-4}$有（ ）
| A． | 最大值8 | B． | 最小值10 | C． | 最大值12 | D． | 最小值14 |
15．设F1，F2是椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}$=1（a1＞b1＞0）与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}$=1（a2＞0，b2＞0）的公共焦点，曲线C1，C2在第一象限内交于点M，∠F1MF2=90°，若椭圆C1的离心率e1∈[$\frac{{\sqrt{6}}}{3}$，1），则双曲线C2的离心率e2的范围是（ ）
| A． | $（{1，\sqrt{3}}]$ | B． | $（{1，\sqrt{2}}]$ | C． | $[{\sqrt{3}，+∞}）$ | D． | $[{\sqrt{2}，+∞}）$ |
12．“x=1”是“x2+x-2=0”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
19．对于任意两个向量$\overrightarrow{a}$，$\overrightarrow{b}$，下列说法正确的是（ ）
| A． | 若$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|＞|$\overrightarrow{b}$|，且$\overrightarrow{a}$与$\overrightarrow{b}$同向，则$\overrightarrow{a}$＞$\overrightarrow{b}$ | B． | 当实数λ=0时，λ$\overrightarrow{a}$=0 | ||
| C． | |$\overrightarrow{a}$•$\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | D． | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |
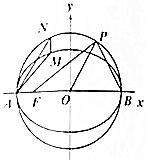已知椭圆C1：$\frac{{x}^{2}}{4}$+y2=1和圆C2：x2+y2=4，A，B，F分别为椭圆C1左顶点、右顶点和左焦点．