题目内容
已知奇函数f(x)满足对于?x∈R,都有f(1+x)=f(1-x),且当x∈[-1,0]时,f(x)=-x2,又函数g(x)=|sinπx|,则函数h(x)=f(x)-g(x)在[-2,2]上的零点个数是( )
| A、4 | B、5 | C、6 | D、7 |
考点:函数零点的判定定理
专题:数形结合,函数的性质及应用
分析:函数零点可看作f(x)与g(x)函数图象的交点,作图可得.
解答:
解:由题意可得函数图象关于x=1对称,
又当x∈[-1,0]时,f(x)=-x2,
可作出f(x)的大致图象,(图中黑色线)
同样,由g(x)=|sinπx|,可得其图象,(图中红色线)
函数h(x)=f(x)-g(x)在[-2,2]上的零点可看作f(x)与g(x)函数图象的交点,
作图可知图象有5个交点,(图中实点)
故选:B

又当x∈[-1,0]时,f(x)=-x2,
可作出f(x)的大致图象,(图中黑色线)
同样,由g(x)=|sinπx|,可得其图象,(图中红色线)
函数h(x)=f(x)-g(x)在[-2,2]上的零点可看作f(x)与g(x)函数图象的交点,
作图可知图象有5个交点,(图中实点)
故选:B

点评:本题考查函数的零点,数形结合是解决问题的关键,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=(x-1)ln(2x-2)的单调递减区间是( )
A、(1,
| ||||
B、(-∞,
| ||||
C、(1,1+
| ||||
D、(-∞,1+
|
已知直线m,l,平面α,β,且m⊥α,l?β,给出下列命题,其中正确的是( )
| A、若α∥β,则m⊥l |
| B、若α⊥β,则m∥l |
| C、若m⊥l,则α∥β |
| D、若m∥l,则α∥β |
若复数z满足z•(1+2i)=1,则
=( )
| z |
A、
| ||||
| B、1-2i | ||||
C、
| ||||
| D、1+2i |
在△ABC中,若A=30°,B=60°,b=
,则a等于( )
| 3 |
| A、3 | ||
| B、1 | ||
| C、2 | ||
D、
|
函数y=|tan2x|是( )
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
2sin105°cos105°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
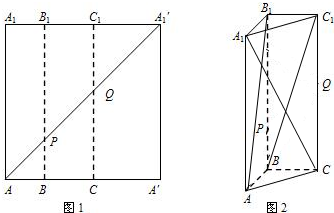 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.