题目内容
已知,函数f(x)=ax2+bx(a,b∈R),g(x)=lnx.函数f(x)的图象能否恒在函数y=bg(x)的上方?若能,求a,b的取值范围;若不能,请说明理由.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:假设函数f(x)的图象恒在函数y=bg(x)的上方,即f(x)>bg(x)在x>0时恒成立.分别对a,b分类讨论,再利用导数研究函数的单调性即可.
解答:
解:假设函数f(x)的图象恒在函数y=bg(x)的上方,即f(x)>bg(x)在x>0时恒成立.
下面分类讨论:
①当a<0时,f(x)图象开口向下,即f(x)>bg(x)在x>0时不可能恒成立,
②a=0时,bx>blnx,
当b>0时,可得x>lnx,此式对于x>0恒成立.
∴b>0时,f(x)>bg(x)恒成立,
b≤0时,f(x)>bg(x)不成立,
③a>0时,
若b<0,则
<
.令h(x)=
(x>0).
下面证明函数h(x)在区间(0,+∞)单调递增.
则h′(x)=
,
再令u(x)=1+x-2lnx,则u′(x)=
,
可知当x=2时,u(x)取得最小值u(2)=3-2ln2>0.
∴h′(x)>0,
因此函数h(x)在区间(0,+∞)单调递增.
可得
无最小值,故f(x)>bg(x)不可能恒成立,
若b=0,则ax2>0,故f(x)>bg(x)恒成立,
若b>0,则ax2+b(x-lnx)>0,故f(x)>bg(x)恒成立,
综上,a=0,b>0或a>0,b≥0时<函数f(x)的图象恒在函数y=bg(x)的图象的上方.
下面分类讨论:
①当a<0时,f(x)图象开口向下,即f(x)>bg(x)在x>0时不可能恒成立,
②a=0时,bx>blnx,
当b>0时,可得x>lnx,此式对于x>0恒成立.
∴b>0时,f(x)>bg(x)恒成立,
b≤0时,f(x)>bg(x)不成立,
③a>0时,
若b<0,则
| a |
| b |
| lnx-x |
| x2 |
| lnx-x |
| x2 |
下面证明函数h(x)在区间(0,+∞)单调递增.
则h′(x)=
| 1+x-2lnx |
| x3 |
再令u(x)=1+x-2lnx,则u′(x)=
| x-2 |
| x |
可知当x=2时,u(x)取得最小值u(2)=3-2ln2>0.
∴h′(x)>0,
因此函数h(x)在区间(0,+∞)单调递增.
可得
| lnx-x |
| x2 |
若b=0,则ax2>0,故f(x)>bg(x)恒成立,
若b>0,则ax2+b(x-lnx)>0,故f(x)>bg(x)恒成立,
综上,a=0,b>0或a>0,b≥0时<函数f(x)的图象恒在函数y=bg(x)的图象的上方.
点评:本题考查了恒成立问题的等价转化方法、利用导数研究函数的单调性极值与最值,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
在△ABC中,若A=30°,B=60°,b=
,则a等于( )
| 3 |
| A、3 | ||
| B、1 | ||
| C、2 | ||
D、
|
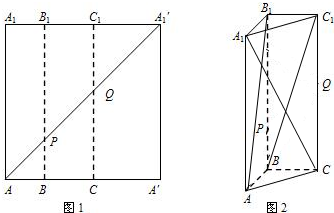 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.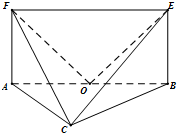 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,△ABC为等边三角形. O为AB的中点,OF⊥EC.