题目内容
△ABC的内角A、B、C的对边分别为a、b、c,sin2A+sin2C-
sinAsinC=sin2B.
(1)求B;
(2)若A=75°,b=2,求△ABC的面积.
| 2 |
(1)求B;
(2)若A=75°,b=2,求△ABC的面积.
考点:余弦定理,正弦定理
专题:三角函数的求值
分析:(1)已知等式利用正弦定理化简,得到关系式,利用余弦定理表示出cosB,将得出的关系式整理后代入计算求出cosB的值,即可确定出B的度数;
(2)由A的度数,求出C的度数,且求出sinA的值,再由sinB,b的值,利用正弦定理求出a的值,利用三角形的面积公式即可求出三角形ABC的面积.
(2)由A的度数,求出C的度数,且求出sinA的值,再由sinB,b的值,利用正弦定理求出a的值,利用三角形的面积公式即可求出三角形ABC的面积.
解答:
解:(1)已知等式sin2A+sin2C-
sinAsinC=sin2B,利用正弦定理化简得:a2+c2-
ac=b2,
∴a2+c2-b2=
ac,
∴cosB=
=
,
则B=45°;
(2)∵A=75°,∴sinA=sin75°=sin(45°+30°)=
,C=60°,
∵sinB=
,b=2,
∴由正弦定理
=
得:a=
=
=
+1,
则S△ABC=
absinC=
×(
+1)×2×
=
.
| 2 |
| 2 |
∴a2+c2-b2=
| 2 |
∴cosB=
| a2+c2-b2 |
| 2ac |
| ||
| 2 |
则B=45°;
(2)∵A=75°,∴sinA=sin75°=sin(45°+30°)=
| ||||
| 4 |
∵sinB=
| ||
| 2 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
2×
| ||||||
|
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
3+
| ||
| 2 |
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
2sin105°cos105°的值为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
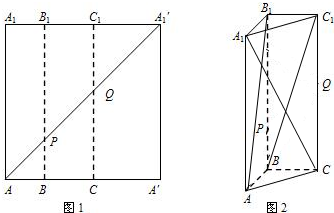 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.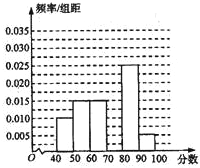 某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题: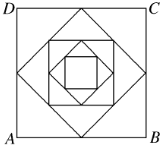 如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?
如图,正方形ABCD的边长是a,依次连接正方形ABCD各边中点得到一个新的正方形,再依次连接新正方形各边中点又得到一个新的正方形,依此得到一系列的正方形,如图所示.现有一只小虫从A点出发,沿正方形的边逆时针方向爬行,每遇到新正方形的顶点时,沿这个正方形的边逆时针方向爬行,如此下去,问爬行2n条线段的长度的平方和是多少?