题目内容
4.一个几何体的三视图如图所示,则该几何体的表面积为( )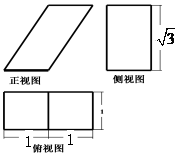
| A. | 2+4$\sqrt{3}$ | B. | 4+4$\sqrt{3}$ | C. | 8+2$\sqrt{3}$ | D. | 6+2$\sqrt{3}$ |
分析 由已知中的三视图可得:该几何体是以正视图为底面的四棱柱,代入柱体表面积公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是以正视图为底面的四棱柱,
故底面面积为:1×$\sqrt{3}$=$\sqrt{3}$,
底面周长C=2(1+$\sqrt{{1}^{2}+{\sqrt{3}}^{2}}$)=6,
棱柱的高h=1,
故棱柱的表面积S=6+2$\sqrt{3}$,
故选:D
点评 本题考查的知识点是棱柱的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
15.下列函数中,是奇函数且在(0,+∞)上单调递减的是( )
| A. | y=x-1 | B. | y=($\frac{1}{2}$)x | C. | y=x3 | D. | $y={log_{\frac{1}{2}}}x$ |
12.有一个几何体的三视图如图所示,这个几何体应是一个( )
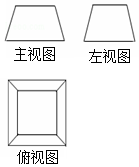

| A. | 棱台 | B. | 棱锥 | C. | 棱柱 | D. | 正四面体 |
16.函数$f(x)=lnx-\frac{2}{x}$的零点所在的大致区间是( )
| A. | (e,+∞) | B. | $(\frac{1}{e},1)$ | C. | (2,3) | D. | (e,+∞) |
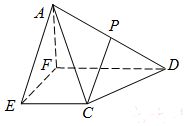 如图,在四棱锥A-CDFE中,底面CDFE是直角梯形,CE∥DF,EF⊥EC,$CE=\frac{1}{2}DF$,AF⊥平面CDFE,P为AD中点.
如图,在四棱锥A-CDFE中,底面CDFE是直角梯形,CE∥DF,EF⊥EC,$CE=\frac{1}{2}DF$,AF⊥平面CDFE,P为AD中点.