题目内容
14.抛物线$x=\frac{1}{4}{y^2}$的焦点到双曲线${x^2}-\frac{y^2}{3}=1$的渐近线的距离是$\frac{\sqrt{3}}{2}$.分析 求出抛物线的焦点坐标,双曲线的焦点坐标到渐近线的距离,转化求解即可.
解答 解:双曲线${x^2}-\frac{y^2}{3}=1$的焦点(2,0)到渐近线$\sqrt{3}$x+y=0距离为:b=$\frac{|2\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+{1}^{2}}}$=$\sqrt{3}⇒x=\frac{1}{4}{y^2}$的焦点(1,0)到渐近线距离为$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查抛物线以及双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
5.命题p:?x>2,2x-3>0的否定是( )
| A. | ?x0>2,${2^{x_0}}-3≤0$ | B. | ?x≤2,2x-3>0 | C. | ?x>2,2x-3≤0 | D. | ?x0>2,${2^{x_0}}-3>0$ |
9.已知P:?x>0,lnx<x,则¬P为( )
| A. | ?x≤0,lnx0>x0 | B. | ?x≤0,lnx0≥x0 | C. | ?x>0,lnx0≥x0 | D. | ?x>0,lnx0<x0 |
3.已知命题α:如果x<3,那么x<5,命题β:如果x≥3,那么x≥5,则命题α是命题β的( )
| A. | 否命题 | B. | 逆命题 | C. | 逆否命题 | D. | 否定形式 |
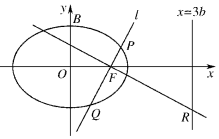 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点F,B分别是椭圆的右焦点与上顶点,O为坐标原点,记△OBF的周长与面积分别为C和S.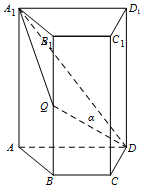 如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,Q为BB1的中点,过A1,Q,D三点的平面记为α.
如图,四棱柱ABCD-A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,Q为BB1的中点,过A1,Q,D三点的平面记为α.