题目内容
以下四个关于圆锥曲线的结论中:
①双曲线
-
=1与椭圆
+y2=1有相同的焦点;
②已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值不存在;
③双曲线
-
=1的左焦点为F1,顶点为A1、A2,P是双曲线上任意一点,则分别以线段PF1、A1A2为直径的两圆的位置关系为内切或外切;
④椭圆
+
=1的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1),(x2,y2),则|y1-y2|值为
;
其中结论正确的序号为 .
①双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
②已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y12+y22的最小值不存在;
③双曲线
| x2 |
| a2 |
| y2 |
| b2 |
④椭圆
| x2 |
| 25 |
| y2 |
| 16 |
| 5 |
| 3 |
其中结论正确的序号为
考点:命题的真假判断与应用
专题:圆锥曲线的定义、性质与方程
分析:根据椭圆、双曲线的定义和性质,结合圆的位置关系,韦达定理等知识点对题目中的四个结论逐一判断,可得答案.
解答:
解:对于①双曲线
-
=1的焦点为(±
,0),椭圆
+y2=1的焦点为(±
,0),故正确;
对于②已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则当直线与x轴垂直时y12+y22的最小值为32,故错误;
对于③设以线段PF1、A1A2为直径的两圆的半径分别为r1、r2,若P在双曲线坐支,如图所示,
则|O1O2|=
|PF2|=
(|PF1|+2a)=
|PF1|+a=r1+r2,即圆心距为半径之和,两圆外切.
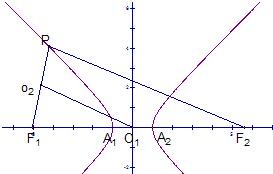
若P在双曲线右支,同理求得|O1O2|=r1-r2,故此时,两圆相内切.故正确;
对于④椭圆
+
=1的左右焦点分别为F1,F2,弦AB过F1,若△ABF2的周长为:20,由内切圆周长为π,可得内切圆半径为:
,
故△ABF2的面积为:5,即c|y1-y2|=3|y1-y2|=5,则|y1-y2|值为
;故正确;
故答案为:①③④
| x2 |
| 25 |
| y2 |
| 9 |
| 34 |
| x2 |
| 35 |
| 34 |
对于②已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则当直线与x轴垂直时y12+y22的最小值为32,故错误;
对于③设以线段PF1、A1A2为直径的两圆的半径分别为r1、r2,若P在双曲线坐支,如图所示,
则|O1O2|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

若P在双曲线右支,同理求得|O1O2|=r1-r2,故此时,两圆相内切.故正确;
对于④椭圆
| x2 |
| 25 |
| y2 |
| 16 |
| 1 |
| 2 |
故△ABF2的面积为:5,即c|y1-y2|=3|y1-y2|=5,则|y1-y2|值为
| 5 |
| 3 |
故答案为:①③④
点评:本题考查圆与圆的位置关系及其判定,椭圆、双曲线的定义和简单性质的应用,考查数形结合思想方法,是中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
焦距为6,离心率e=
,焦点在x轴上的椭圆标准方程是( )
| 3 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}是公差不为零的等差数列,a1=2,且a2,a4,a8成等比数列.
(I)求数列{an}的通项;
(Ⅱ)设数列{bn-an}是等比数列,且b2=7,b5=91,求数列{bn}的前n项和Tn.
(I)求数列{an}的通项;
(Ⅱ)设数列{bn-an}是等比数列,且b2=7,b5=91,求数列{bn}的前n项和Tn.
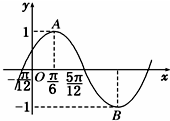 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
| A、y=sin 2x | ||
| B、y=cos 2x | ||
C、y=sin(2x+
| ||
D、y=sin(2x-
|
三角形ABC的三内角A、B、C所对的边长分别是a,b,c若(a+b)(sinB-sinA)=(
a+c)sinC,则角B的大小为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|