题目内容
给出下列各函数值:①sin(-1 000°);②cos(-2 200°);③tan(-10);④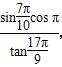 ,其中符号为负的是( )
,其中符号为负的是( )
A.① B.②
C.③ D.④
C

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
题目内容
给出下列各函数值:①sin(-1 000°);②cos(-2 200°);③tan(-10);④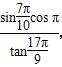 ,其中符号为负的是( )
,其中符号为负的是( )
A.① B.②
C.③ D.④
C

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案