题目内容
已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)如果函数g(x)的单调递减区间为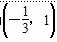 ,求函数g(x)的解析式;
,求函数g(x)的解析式;
(2)在(1)的条件下,求函数y=g(x)的图像在点P(-1,1)处的切线方程;
(3)若不等式2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
解:(1)g′(x)=3x2+2ax-1,由题意得3x2+2ax-1<0的解集是 ,
,
即3x2+2ax-1=0的两根分别是-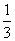 ,1.
,1.
将x=1或x=-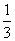 代入方程3x2+2ax-1=0,得a=-1.∴g(x)=x3-x2-x+2.
代入方程3x2+2ax-1=0,得a=-1.∴g(x)=x3-x2-x+2.
(2)由(1)知,g′(x)=3x2-2x-1,
∴g′(-1)=4,∴点P(-1,1)处的切线斜率k=g′(-1)=4,
∴函数y=g(x)的图像在点P(-1,1)处的切线方程为y-1=4(x+1),即4x-y+5=0.
(3)∵f(x)的定义域为(0,+∞),∴2f(x)≤g′(x)+2恒成立,即2xln x≤3x2+2ax+1对x∈(0,+∞)上恒成立.
可得a≥ln x- -
- 在x∈(0,+∞)上恒成立.
在x∈(0,+∞)上恒成立.
令h(x)=ln x- -
- ,
,
则h′(x)=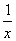 -
- +
+ =-
=- .
.
令h′(x)=0,得x=1或x=-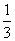 (舍).
(舍).
当0<x<1时,h′(x)>0;
当x>1时,h′(x)<0.
∴当x=1时,h(x)取得最大值,
h(x)max=h(1)=-2,
∴a≥-2.∴a的取值范围是[-2,+∞).

练习册系列答案
相关题目

 D.[1,2)
D.[1,2)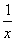 在
在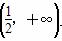 上是增函数,则a的取值范围是( )
上是增函数,则a的取值范围是( )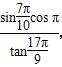 ,其中符号为负的是( )
,其中符号为负的是( ) 的坐标为________.
的坐标为________.
 ”的________条件.
”的________条件. ___ .
___ .