题目内容
已知函数f(x)=(x2-ax)ex(x∈R),a为实数.
(1)当a=0时,求函数f(x)的单调增区间;
(2)若f(x)在闭区间[-1,1]上为减函数,求a的取值范围.
解:(1)当a=0时,f(x)=x2ex,f′(x)=2xex+x2ex=(x2+2x)ex,由f′(x)>0⇒x>0或x<-2,故f(x)的单调增区间为(0,+∞)和(-∞,-2).
(2)由f(x)=(x2-ax)ex,x∈R
⇒f′(x)=(2x-a)ex+(x2-ax)ex=[x2+(2-a)x-a]ex.
记g(x)=x2+(2-a)x-a,
依题意,x∈[-1,1]时,g(x)≤0恒成立,
结合g(x)的图像特征得
即a≥ ,所以a的取值范围是
,所以a的取值范围是 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 时,n≤f(x)≤m恒成立,则m-n的最小值为( )
时,n≤f(x)≤m恒成立,则m-n的最小值为( )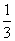 B.
B.
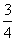 D.1
D.1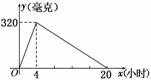 某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图像,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )
某种新药服用x小时后血液中的残留量为y毫克,如图所示为函数y=f(x)的图像,当血液中药物残留量不小于240毫克时,治疗有效.设某人上午8:00第一次服药,为保证疗效,则第二次服药最迟的时间应为( )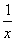 在
在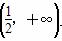 上是增函数,则a的取值范围是( )
上是增函数,则a的取值范围是( )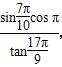 ,其中符号为负的是( )
,其中符号为负的是( )