题目内容
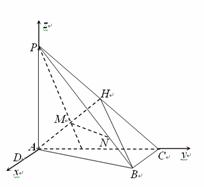
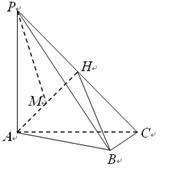 如图,在三棱锥
如图,在三棱锥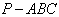 中,
中,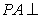 底面
底面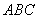 ,
,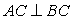 ,
,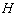 为
为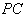 的中点,
的中点,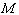 为
为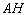 的中点,
的中点,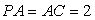 ,
,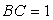 .
.
(Ⅰ)求证: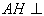 平面
平面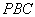 ;
;
(Ⅱ)求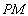 与平面
与平面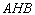 成角的正弦值;
成角的正弦值;
(Ⅲ)设点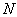 在线段
在线段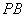 上,且
上,且 ,
,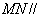 平面
平面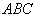 ,
,
求实数 的值.
的值.
(Ⅰ)证明:因为 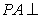 底面
底面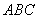 ,
,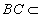 底面
底面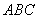 ,
,
所以 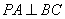 , ………… 1分
, ………… 1分
又因为 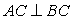 ,
, 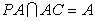 , 所以
, 所以 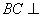 平面
平面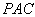 ,………… 2分
,………… 2分
又因为 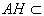 平面
平面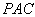 , 所以
, 所以 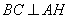 . ……… 3分
. ……… 3分
因为 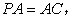
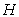 是
是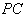 中点,所以
中点,所以 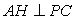 ,
,
又因为 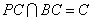 ,所以
,所以 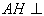 平面
平面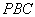 . …………… 5分
. …………… 5分
(Ⅱ)解:在平面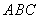 中,过点
中,过点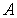 作
作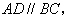
因为 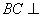 平面
平面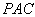 ,所以
,所以 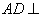 平面
平面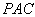 ,
,
由 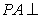 底面
底面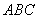 ,得
,得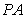 ,
,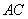 ,
, 两两垂直,
两两垂直,
所以以 为原点,
为原点, ,
,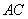 ,
,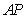 所在直线分别为x轴,y轴,z轴如图建立空间直角坐标系,则
所在直线分别为x轴,y轴,z轴如图建立空间直角坐标系,则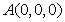 ,
,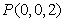 ,
,
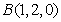 ,
,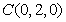 ,
,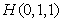 ,
,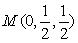
设平面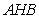 的法向量为
的法向量为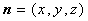 , 因为
, 因为 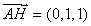 ,
,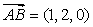 ,
,
 由
由 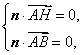 得
得 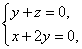 令
令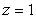 ,得
,得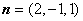 .………… 7分
.………… 7分
设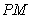 与平面
与平面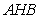 成角为
成角为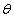 , 因为
, 因为 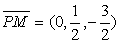 ,
,
所以 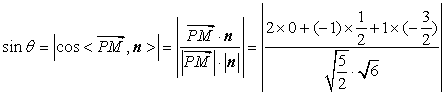 ,
,
即 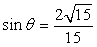 . …… 9分
. …… 9分
(Ⅲ)解:因为 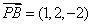 ,
,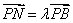 , 所以
, 所以 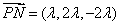 ,
,
又因为 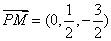 ,所以
,所以 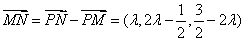 . … 11分
. … 11分
因为 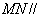 平面
平面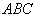 ,平面
,平面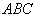 的法向量
的法向量 ,
,
所以 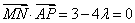 , 解得
, 解得  . ……… 13分
. ……… 13分

练习册系列答案
相关题目
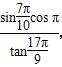 ,其中符号为负的是( )
,其中符号为负的是( ) ,等比数列
,等比数列 中,
中, ,则
,则 ( )
( ) ___ .
___ .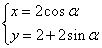
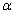 为参数),M是C1上的动点,P点满足
为参数),M是C1上的动点,P点满足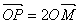 ,P点的轨迹为曲线C2,
,P点的轨迹为曲线C2,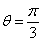 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求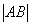 .
. B.
B. C.
C. D.
D.

 ,其中
,其中 是实数,
是实数, 是虚数单位,则
是虚数单位,则 的共轭复数为( )
的共轭复数为( ) B.
B. C.
C. D.
D.
 .
. 的单调区间;
的单调区间; 时,若方程
时,若方程 在
在 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围; .
.