题目内容
1.已知数列{an}中a1=1,nan=(n+1)an+1,则a2016=$\frac{1}{2016}$.分析 a1=1,nan=(n+1)an+1,可得$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.利用“累乘求积”即可得出.
解答 解:∵a1=1,nan=(n+1)an+1,
∴$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n}{n+1}$.
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{2}}{{a}_{1}}$•a1
=$\frac{n-1}{n}$•$\frac{n-2}{n-1}$•…•$\frac{1}{2}$•1
=$\frac{1}{n}$.
∴a2016=$\frac{1}{2016}$.
故答案为:$\frac{1}{2016}$.
点评 本题考查了递推关系、“累乘求积”的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
16.一个三棱锥的三视图如图所示,则该三棱锥的体积为( )
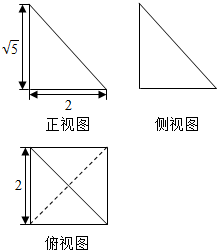

| A. | $\frac{2\sqrt{5}}{3}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |