题目内容
6.已知数列{an}是各项均不为0的等差数列,Sn为其前n项和,且满足an2=S2n-1,bn=$\frac{1}{a{{\;}_{n}a}_{n+1}}$.(1)求数列{an}、{bn}的通项公式及其前n项和Tn;
(2)在数列{bn}中,是否存在正整数m,n(1<m<n),使得T1,Tm,Tn依次成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
分析 (1)根据递推关系求出a1,a2,即可求出公差,整理后可求得an,代入利用裂项法求得Tn.
(2)根据(1)中求得Tn分别表示出T1,Tm,Tn根据等比中项的性质建立等式,化简整理即可求得m的范围,进而根据m和n均为正整数求得m,进而n
解答 解:(1):n=1时,${a}_{1}^{2}={S}_{1}={a}_{1}$≠0,解得a1=1.
n=2时,${a}_{2}^{2}={S}_{3}$,∴(1+d)2=3+3d,解得d=2或-1.
d=-1时,a2=0,舍去.
∴d=2.
∴an=1+2(n-1)=2n-1,
bn=$\frac{1}{a{{\;}_{n}a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
由Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$,
(2)由(1)知,Tn=$\frac{n}{2n+1}$,
∴T1=$\frac{1}{3}$,Tm=$\frac{m}{2m+1}$,
若T1,Tm,Tn依次成等比数列,
则($\frac{m}{2m+1}$)2=$\frac{1}{3}$•$\frac{n}{2n+1}$,
整理可得$\frac{3}{n}$=$\frac{-2{m}^{2}+4m+1}{{m}^{2}}$
∴-2n2+4m+1>0,
解得1-$\frac{\sqrt{6}}{2}$<m<1+$\frac{\sqrt{6}}{2}$,
又m∈N,且m>1,
所以m=2,此时n=12.
故可知:当且仅当m=2,n=12使数列{Tn}中的T1,Tm,Tn成等比数列.
点评 本题考查了等差数列的通项公式与求和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $[{\frac{1}{e^2},1}]$ | B. | $[{\frac{2}{e},1}]$ | C. | $[{\frac{1}{e},1}]$ | D. | [1,e] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 0 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 1 |
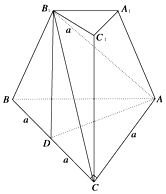 三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,
三棱台ABC-A1B1C1中,侧棱CC1⊥底面ABC,∠ACB=90°,AC=B1C1=a,BC=2a,AB1与CC1成45°角,D为BC中点,