题目内容
17.已知函数f(x)=x3-2x2+x,将函数y=|f(x)|的图象沿着x轴作对称变换得到函数y=g(x)的图象,函数h(x)=$\left\{\begin{array}{l}g(x),x<1\\ lnx,x≥1\end{array}$,若关于x的不等式h(x)-kx≤0在R上恒成立,则实数k的取值范围是( )| A. | $[{\frac{1}{e^2},1}]$ | B. | $[{\frac{2}{e},1}]$ | C. | $[{\frac{1}{e},1}]$ | D. | [1,e] |
分析 由题意画出函数h(x)与y=kx的图象,再由导数求出直线y=kx与y=h(x)相切的切线斜率得答案.
解答 解:由f(x)=x3-2x2+x,得f′(x)=3x2-4x+1,
由f′(x)=0,得x=$\frac{1}{3}$或x=1,
当x∈(-∞,$\frac{1}{3}$),(1,+∞)时,f(x)为增函数,当x∈($\frac{1}{3},1$)时,f(x)为减函数,
不等式h(x)-kx≤0在R上恒成立,即h(x)≤kx在R上恒成立,
作出函数y=h(x)与y=kx的图象如图: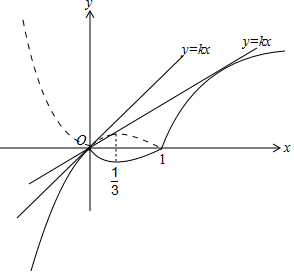
设y=kx与y=lnx相切于(x0,lnx0),$y′{|}_{x={x}_{0}}=\frac{1}{{x}_{0}}$,
则切线方程为y-$ln{x}_{0}=\frac{1}{{x}_{0}}(x-{x}_{0})$,代入(0,0)得:-lnx0=-1,得x0=e,
∴k=$\frac{1}{e}$;
由f(x)=x3-2x2+x,得f′(x)=3x2-4x+1,
可得f′(0)=1,即y=h(x)在原点处的切线的斜率为1.
∴实数k的取值范围是[$\frac{1}{e},1$].
故选:C.
点评 本题考查函数恒成立问题,考查数形结合的解题思想方法和数学转化思想方法,属中档题.

练习册系列答案
相关题目
5.已知集合A={x|x2+2x<0},B={x|($\frac{1}{2}$)x-2≥0},则A∩B=( )
| A. | (-2,-1) | B. | (-1,0) | C. | (-2,-1] | D. | [-1,0) |
 如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=$\frac{1}{2}$.
如图,在△ABC中,H为BC上异于B,C的任一点,M为AH的中点,若$\overrightarrow{AM}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AC}$,则λ+μ=$\frac{1}{2}$.