题目内容
1.已知f(x)=x3+(a-1)x2是奇函数,则不等式f(ax)>f(a-x)的解集是{x|x>$\frac{1}{2}$}.分析 根据函数的奇偶性求出a的值,根据函数的单调性问题转化为x>1-x,解不等式即可.
解答 解:若f(x)=x3+(a-1)x2是奇函数,
则a-1=0,即a=1,此时f(x)=x3,在R递增,
则不等式f(ax)>f(a-x),
即x>1-x,解得:x>$\frac{1}{2}$,
故不等式的解集是:{x|x>$\frac{1}{2}$},
故答案为:{x|x>$\frac{1}{2}$}.
点评 本题考查了函数的奇偶性和单调性问题,是一道基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
12.设a,b是非零实数,若a>b,则一定有( )
| A. | $a+\frac{1}{b}>b+\frac{1}{a}$ | B. | $\frac{1}{{a{b^2}}}>\frac{1}{{{a^2}b}}$ | C. | $\frac{1}{a}<\frac{1}{b}$ | D. | ab>b2 |
6.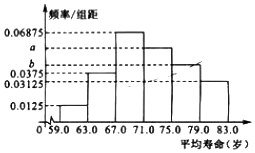 下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
(Ⅰ)请补齐频率分布表,并求出相应频率分布直方图中的a,b;
(Ⅱ)请根据统计思想,利用(Ⅰ)中的频率分布直方图估计亚洲人民的平均寿命.
 下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)| 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
| 阿曼 76.1 巴林 76.1 朝鲜 68.9 韩国 80.6 老挝 64.3 蒙古 67.6 缅甸 64.9 日本 82.8 | 泰国 73.7 约旦 73.4 越南 75.0 中国 74.8 伊朗 74.0 印度 66.5 文莱 77.6 也门 62.8 | 阿富汗 59.0 阿联酋 76.7 东帝汶 67.3 柬埔寨 66.4 卡塔尔 77.8 科威特 74.1 菲律宾 67.8 黎巴嫩 78.5 | 尼泊尔 68.0 土耳其 74.1 伊拉克 68.5 以色列 81.6 新加坡 81.5 叙利亚 72.3 巴基斯坦 65.2 马来西亚 74.2 | 孟加拉国 70.1 塞浦路斯 79.4 沙特阿拉伯 73.7 哈萨克斯坦68.3 印度尼西亚68.2 土库曼斯坦65.0 吉尔吉斯斯坦69.3 乌兹别克斯坦67.9 |
| 分组 | 频数 | 频率 |
| [59.0,63.0) | 2 | 0.05 |
| [63.0,67.0) | 6 | 0.15 |
| [67.0,71.0) | 11 | 0.275 |
| [71.0,75.0) | 9 | 0.225 |
| [75.0,7.0) | 7 | 0.175 |
| [79.0,83.0] | 5 | 0.125 |
| 合计 | 40 | 1.00 |
13.已知a=0.993,b=log20.6,c=log3π,则( )
| A. | c<a<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
11.已知点P(a,b)关于直线l的对称点为Q(3-b,3-a),则直线l的方程是( )
| A. | x+y-3=0 | B. | x+y+b-a=0 | C. | x+y-a-b=0 | D. | x-y+3=0 |
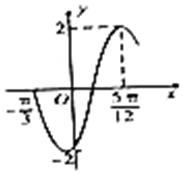 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示.