题目内容
9.设$f(x)=\left\{{\begin{array}{l}{2{e^{x-1}},x<2}\\{{{log}_3}•({2^x}-1),x≥2}\end{array}}\right.$,则f[f(2)]等于( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由题意先求出f(2)=log3(4-1)=1,从而f[f(2)]=f(1),由此能求出结果.
解答 解:∵$f(x)=\left\{{\begin{array}{l}{2{e^{x-1}},x<2}\\{{{log}_3}({2^x}-1),x≥2}\end{array}}\right.$,
∴f(2)=log3(4-1)=1,
f[f(2)]=f(1)=2e1-1=2.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
17.已知函数$f(n)=\left\{\begin{array}{l}{n^2}(当n为奇数时)\\-{n^2}(当n为偶数时)\end{array}\right.$且an=f(n)+f(n+1),则a1+a2+…+a99等于( )
| A. | 0 | B. | 100 | C. | -101 | D. | -99 |
14.已知全集U={1,2,3,4,5},集合A={3,4},B={1,2},则(∁UA)∩B等于( )
| A. | {1,2} | B. | [1,3} | C. | {1,2,5} | D. | {1,2,3} |
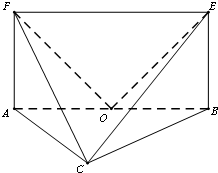 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.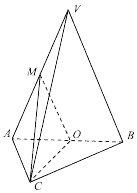 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.