题目内容
若(1-2x)2012=a0+a1x+a2x2+…+a2012x2012(x∈R),则a0+(a0+a1)+(a0+a2)+…+(a0+a2012)= .
考点:二项式定理
专题:二项式定理
分析:在所给的等式中,令x=0求得a0=1;再令x=1,可得 a0+a1 +a2 +…+a2012 =1,由此求得所求式子的值.
解答:
解:在(1-2x)2012=a0+a1x+a2x2+…+a2012x2012(x∈R)中,令x=0,可得a0=1,
再令x=1,可得 a0+a1 +a2 +…+a2012 =1,
∴a0+(a0+a1)+(a0+a2)+…+(a0+a2012)=2012a0+[a0+a1 +a2 +…+a2012 ]=2012+1=2013,
故答案为:2013.
再令x=1,可得 a0+a1 +a2 +…+a2012 =1,
∴a0+(a0+a1)+(a0+a2)+…+(a0+a2012)=2012a0+[a0+a1 +a2 +…+a2012 ]=2012+1=2013,
故答案为:2013.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
相关题目
若(x+
)n展开式中只有第6项的系数最大,则常数项是( )
| 1 |
| x |
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
已知向量
与
的夹角为为30°,且|
|=
,|
|=2,则|
+
|=( )
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=2ln3x+8x,则
的值为( )
| lim |
| △x→0 |
| f(1+2△x)-f(1) |
| △x |
| A、-20 | B、-10 |
| C、10 | D、20 |
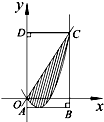 如图,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为
如图,矩形ABCD内的阴影部分是由曲线f(x)=2x2-2x及直线y=2x围成的,现向矩形ABCD内随机投掷一点,则该点落在阴影部分的概率为