题目内容
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知ccosB=(2a-b)cosC.(1)求角C的大小;
(2)若AB=4,求△ABC的面积S的最大值.
分析 (1)已知等式利用正弦定理化简,再利用诱导公式变形,求出cosC的值,即可确定出C的度数;
(2)由c与C的度数,表示出三角形ABC面积,利用余弦定理及基本不等式求出ab的最大值,进而确定出三角形ABC面积的最大值,以及此时三角形的形状即可.
解答 解:(1)∵ccosB=(2a-b)cosC,
∴由正弦定理可知,sinCcosB=2sinAcosC-sinBcosC,
即sinCcosB+cosCsinB=2sinAcosC,
∴sin(C+B)=2sinAcosC,
∵A+B+C=π,∴sinA=2sinAcosC,
∵sinA≠0,
∴cosC=$\frac{1}{2}$,
∵0<C<π,
∴C=$\frac{π}{3}$;
(2)由题可知c=AB=4,C=$\frac{π}{3}$;
S△ABC=$\frac{1}{2}$absinC=$\frac{\sqrt{3}}{4}$ab,
由余弦定理可知:a2+b2=c2+2abcosC,即a2+b2=16+ab≥2ab,
∴ab≤16,当且仅当a=b时取等号,
∴S△ABC的最大值4$\sqrt{3}$,
此时三角形为等边三角形.
点评 此题考查正弦、余弦定理的综合应用,涉及三角函数中的恒等变换应用,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
13.设f(x)=$\left\{\begin{array}{l}{a^x},x≥0\\{log_a}({{x^2}+{a^2}}),x<0\end{array}$,且f(2)=4,则f(-2)等于( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知sinα+cosα=$\frac{1-\sqrt{3}}{2}$,且0<α<π,则tanα的值为( )
| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
20.已知球的直径SC=2,A,B是该球球面上的两点,AB=1,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( )
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
 已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.
已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.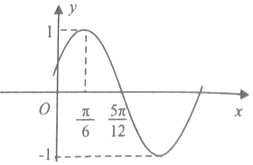 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,