��Ŀ����
4��ŵ���������������˵����ն���7��1�գ�2006��7��1����������������ף�Լ������գ�ŵ����������˵������������ǵ�������������ֶԵ�һ�£�����������䣮�������ش��������������ǵ�һ�η����ˣ���һ�η�������������������Һ����������һ�죮��ŵ����˵�����ǵģ�ȷʵ���������Ҽǵú������������������һ������
����ζԻ��У������ƶϳ�ŵ�����Ľ�������������һ�������
���� �����⣬ŵ����������������ֱ�Ϊ10a+b��10b+a��2006������������������ֱ�Ϊ��10a+b+c��10b+a+c���ɴ˿ɵ÷��̣����ɵó����ۣ�
��� �⣺�����⣬ŵ����������������ֱ�Ϊ10a+b��10b+a��
2006������������������ֱ�Ϊ��10a+b+c��10b+a+c��
�ࣨ10a+b+c+10b+a+c����2=11n��
��cmin=11��
��ŵ�����Ľ�����������1995��7��1�ţ�
���� ���⿼��������ѧ֪ʶ���ʵ�����⣬����ѧ�������������������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
5��ѧУij�ľ��̵꾭Ӫij���ľߣ��̵�ÿ����һ�����ľ߿ɻ���3Ԫ�����������������۴�����ÿ����һ���ľ߿���1Ԫ��������Ӧ������Դ��ⲿ������Ӧ����ʱÿ���ľ߽�����2Ԫ��Ϊ���˽��г�����������������ͳ����ȥ��һ�꣨52�ܣ������������
��ȥ��ÿ�ܵ���������Ƶ��Ϊ����ÿ���г��������ĸ��ʣ�
��1��Ҫʹ�������������г��������ĸ��ʴ���0.5���ʽ����������ֵ�Ƕ��٣�
��2�����������ܽ�����Ϊ14��д��������Y�ķֲ��У�
��3������������������ֵΪ������������ݣ�������ܽ�������Ϊ���ٺ��ʣ�
| ������������ | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| ���� | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
��1��Ҫʹ�������������г��������ĸ��ʴ���0.5���ʽ����������ֵ�Ƕ��٣�
��2�����������ܽ�����Ϊ14��д��������Y�ķֲ��У�
��3������������������ֵΪ������������ݣ�������ܽ�������Ϊ���ٺ��ʣ�
15����֪4cos����+$\frac{��}{3}$��cos����-$\frac{��}{6}$��=sin2�ȣ���tan��2��-$\frac{��}{6}$�����ڣ�������
| A�� | $\frac{1}{6}$ | B�� | $\frac{\sqrt{3}}{9}$ | C�� | -$\frac{\sqrt{3}}{6}$ | D�� | -$\frac{\sqrt{3}}{3}$ |
9���±��ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���x���֣�����Ӧ�������ܺ�y���ֱ�ú���ļ���������ݣ�
��1��������ϱ��ṩ�����ݣ����y����x�Ļع�ֱ�߷��̣�
��2����֪�ó�����ǰ100�ּײ�Ʒ�������ܺ�Ϊ90�ֱ�ú���Ը��ݣ�2������Ļع�ֱ�߷��̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ���Ͷ��ٶֱ�ú��
����$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��a=$\overline{y}$-$\widehat{b}$$\overline{x}$��
| x | 3 | 4 | 5 | 6 | 7 |
| y | 2.5 | 3 | 4 | 4.5 | 6 |
��2����֪�ó�����ǰ100�ּײ�Ʒ�������ܺ�Ϊ90�ֱ�ú���Ը��ݣ�2������Ļع�ֱ�߷��̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ���Ͷ��ٶֱ�ú��
����$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$��a=$\overline{y}$-$\widehat{b}$$\overline{x}$��
16����֪f��x��=$\frac{��x+2��^{0}}{x+1}$����f��x���Ķ������ǣ�������
| A�� | {x|x��-2} | B�� | {x|x��-1} | C�� | {x|x��-1��x��-2} | D�� | {x|x��-1��x��-2} |
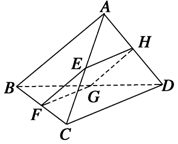 ��ͼ��ʾ���ı���ABCDΪ�ռ��ı��Σ�
��ͼ��ʾ���ı���ABCDΪ�ռ��ı��Σ�