题目内容
2.已知函数f(x)=-x3+x2+b,g(x)=alnx.(1)若f(x)在(1,b)处的切线过点(2,1),求实数b的值;
(2)若对任意x∈[1,e],都有g(x)≥-2x2+(a+4)x恒成立,求实数a的取值范围.
分析 (1)利用导数,令f'(1)=-1,得到切线方程,利用f(x)在(1,b)处的切线过点(2,1),即可解得b的值;
(2)由g(x)≥-2x2+(a+4)x分离出参数a后,转化为求函数最值,利用导数可求最值.
解答 解:(1)由f(x)=-x3+x2+b,得f'(x)=-3x2+2x=-x(3x-2),
令f'(1)=-1,则切线方程为y-b=-(x-1),即x+y-1-b=0.
又∵切线过点(2,1),∴2+1-1-b=0,
∴b=2.
(2)由g(x)≥-2x2+(a+4)x,得(x-lnx)a≤2x2-4x.
∵x∈[1,e],∴lnx≤1≤x,且等号不能同时取,
∴lnx<x,即x-lnx>0,
∴a≤$\frac{2{x}^{2}-4x}{x-lnx}$恒成立,
即a≤( $\frac{2{x}^{2}-4x}{x-lnx}$)min.
令t(x)=$\frac{2{x}^{2}-4x}{x-lnx}$,x∈[1,e],
求导得,t′(x)=$\frac{2(x-1)(x+2-lnx)}{(x-lnx)^{2}}$,
当x∈[1,e]时,x-1≥0,lnx≤1,x+2-lnx>0,从而t′(x)≥0,
∴t(x)在[1,e]上为增函数,tmin(x)=t(1)=-2,
∴a≤-2.
点评 该题考查利用导数研究切线方程、函数的最值、函数恒成立问题,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
相关题目
11.△ABC中,如果cosAcosB>sinAsinB,则△ABC为( )
| A. | 钝角三角形 | B. | 直角三角形 | ||
| C. | 锐角三角形 | D. | 锐角或直角三角形 |
 已知圆心为F1的圆的方程为(x+2)2+y2=32,F2(2,0),C是圆F1上的动点,F2C的垂直平分线交F1C于D.
已知圆心为F1的圆的方程为(x+2)2+y2=32,F2(2,0),C是圆F1上的动点,F2C的垂直平分线交F1C于D.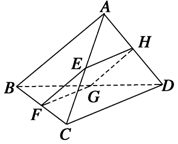 如图所示,四边形ABCD为空间四边形.
如图所示,四边形ABCD为空间四边形.