题目内容
7. 已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.
已知定义在R上的奇函数f(x),当x>0时,f(x)的表达式是二次函数,且f(1)=0,f(3)=0,f(2)=-1.(1)求f(x),x∈(0,+∞)的表达式
(2)画函数y=f(x),x∈R的图象
(3)说出函数y=f(x),x∈(-5,-1]的值域.
分析 (1)设出二次函数的解析式,利用已知条件求解即可.
(2)利用函数的奇偶性,画出函数的图象即可.
(3)利用函数的图象,直接写出函数的值域即可.
解答  解:(1)当x>0时,f(x)的表达式是二次函数,
解:(1)当x>0时,f(x)的表达式是二次函数,
f(1)=0,f(3)=0,
设f(x)=a(x-1)(x-3),又f(2)=-1,可得a=1,
所以f(x)=x2-4x+3,(x>0)
(2)函数y=f(x),x∈R的图象如下:
(3)由图可知函数y=f(x),x∈(-5,-1]的值域为(-8,1].
点评 本题考查二次函数的性质,函数的图象的判断与应用,考查转化思想以及数形结合的应用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
15.已知4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=sin2θ,则tan(2θ-$\frac{π}{6}$)等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
16.已知f(x)=$\frac{(x+2)^{0}}{x+1}$,则f(x)的定义域是( )
| A. | {x|x≠-2} | B. | {x|x≠-1} | C. | {x|x≠-1且x≠-2} | D. | {x|x≠-1或x≠-2} |
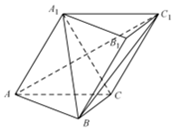 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,底面ABC是等腰直角三角形,CA=CB,A1B⊥AC1.