题目内容
3.已知sinα+cosα=$\frac{1-\sqrt{3}}{2}$,且0<α<π,则tanα的值为( )| A. | -$\frac{\sqrt{3}}{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
分析 由题意根据正弦函数和余弦函数的图象和性质可以判断$\frac{3π}{4}$<α<π,得到$\frac{3π}{2}$<2α<2π,即可求出α=$\frac{5}{6}$π,问题得以解决
解答 解∵sinα+cosα=$\frac{1-\sqrt{3}}{2}$<0,0<α<π,
∴sinα>0,cosα<0,
∴$\frac{3π}{4}$<α<π,
∴$\frac{3π}{2}$<2α<2π,:
∵sinα+cosα=$\frac{1-\sqrt{3}}{2}$,
两边平方可得1+2sinαcosα=$\frac{2-\sqrt{3}}{2}$,
∴2sinαcosα=-$\frac{\sqrt{3}}{2}$=sin2α
∴2α=$\frac{5π}{3}$,
∴α=$\frac{5}{6}$π,
∴tanα=tan$\frac{5π}{6}$=-$\frac{\sqrt{3}}{3}$
故选:A
点评 本题考查同角三角函数关系,考查学生的计算能力,正确判断角的范围是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
| 销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
8.已知函数f(x-1)=x2-2x,且f(a)=3,则实数a的值等于( )
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | 2 | D. | ±2 |
15.已知4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=sin2θ,则tan(2θ-$\frac{π}{6}$)等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
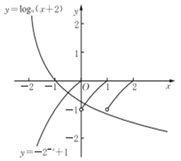 已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).
已知函数$f(x)=\left\{\begin{array}{l}-{2^{-x}}+1,x≤0\\ f(x-1),x>0\end{array}\right.$,若方程f(x)=loga(x+2)(0<a<1)有且仅有两个不同的实数根,则实数a的取值范围为[$\frac{1}{3},\frac{1}{2}$).