题目内容
20.已知球的直径SC=2,A,B是该球球面上的两点,AB=1,∠ASC=∠BSC=30°,则棱锥S-ABC的体积为( )| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{3}}}{6}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 取SC的中点D,则D为球心,过A做AE⊥SC与E,连接BE,则BE⊥SC,∠BED=60°,棱锥S-ABC的体积:VS-ABC=VS-ABE+VC-ABE=$\frac{1}{3}×SC×{S}_{△ABE}$,由此能求出结果.
解答 解:取SC的中点D,则D为球心,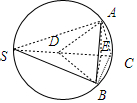
则AD=BD=DS=1,∠ASC=∠BSC=∠SBD=30°,△ASC≌△BSC,
过A做AE⊥SC与E,连接BE,则BE⊥SC,∠BED=60°,
在△BDE中,DE=BDcos∠BED=$\frac{1}{2}$,
BE=BDsin∠BED=$\frac{\sqrt{3}}{2}$,
∴${S}_{△ABE}=\frac{1}{2}×AB×\sqrt{B{E}^{2}-(\frac{AB}{2})^{2}}$=$\frac{1}{2}×1×\sqrt{\frac{3}{4}-\frac{1}{4}}$=$\frac{\sqrt{2}}{4}$,
故三棱锥S-ABC的体积等于棱锥S-ABE和棱锥C-ABE的体积之和,
即棱锥S-ABC的体积:
VS-ABC=VS-ABE+VC-ABE
=$\frac{1}{3}×SE×{S}_{△ABE}+\frac{1}{3}×CE×{S}_{△ABE}$
=$\frac{1}{3}×SC×{S}_{△ABE}$=$\frac{1}{3}×2×\frac{\sqrt{2}}{4}$=$\frac{\sqrt{2}}{6}$.
故选:A.
点评 本题考查柱、锥、台体的体积,解答此题的关键是注意球、锥体的性质的应用,考查空间想象能力与计算能力,考查等价转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
1.函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图,f($\frac{π}{2}$)=-1,则f(0)的值为( )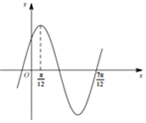

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
8.已知函数f(x-1)=x2-2x,且f(a)=3,则实数a的值等于( )
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | 2 | D. | ±2 |
15.已知4cos(θ+$\frac{π}{3}$)cos(θ-$\frac{π}{6}$)=sin2θ,则tan(2θ-$\frac{π}{6}$)等于( )
| A. | $\frac{1}{6}$ | B. | $\frac{\sqrt{3}}{9}$ | C. | -$\frac{\sqrt{3}}{6}$ | D. | -$\frac{\sqrt{3}}{3}$ |
5.已知全集为U=R,集合B={x|($\frac{1}{2}$)x≤1},A={x|x≥2},则(∁UA)∩B=( )
| A. | [0,2) | B. | [0,2] | C. | (1,2) | D. | (1,2] |
9.下表提供了某厂节能降耗技术改造后,生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:
(1)请根据上表提供的数据,求出y关于x的回归直线方程;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| x | 3 | 4 | 5 | 6 | 7 |
| y | 2.5 | 3 | 4 | 4.5 | 6 |
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.