题目内容
已知|
|=2cos12°,|
|=4cos24°cos48°,
,
的夹角96°为,则
•
的值为 .
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算法则和倍角公式即可得出.
解答:
解:∵|
|=2cos12°,|
|=4cos24°cos48°,
,
的夹角96°,
∴
•
=|
| |
|cos96°=2cos12°•4cos24°cos48°cos96°
=
=
=
=
=
=
=-
.
故答案为:-
.
| a |
| b |
| a |
| b |
∴
| a |
| b |
| a |
| b |
=
| 8×2sin12°cos12°cos24°cos48°cos96° |
| 2sin12° |
=
| 4×2sin24°cos24°cos48°cos96° |
| 2sin12° |
=
| 2×2sin48°cos48°cos96° |
| 2sin12° |
=
| 2sin96°cos96° |
| 2sin12° |
=
| sin192° |
| 2sin12° |
=
| -sin12° |
| 2sin12° |
=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了数量积运算法则和倍角公式,属于基础题.

练习册系列答案
相关题目
已知f(x)是定义在R上的奇函数,且x>0时,f(x)=x2-2x-3,若方程f(x)=a有两个根,则实数a的取值范围是( )
| A、[-4,4] |
| B、[-3,0)∪(0,3]∪{-4,4} |
| C、[-3,3]∪{-4,4} |
| D、(-4,4) |
已知锐角△ABC中,角A、B、C所对边分别为a、b、c,若cos2C=1-
,则角B的大小为( )
| c2 |
| b2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
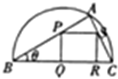 如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.
如图所示,在直径为BC的半圆中,A是弧BC上一点,正方形PQRS内接于△ABC,若BC=a,∠ABC=θ,设△ABC的面积为Sl,正方形PQRS的面积为S2.