题目内容
已知f(x)是定义在R上的奇函数,且x>0时,f(x)=x2-2x-3,若方程f(x)=a有两个根,则实数a的取值范围是( )
| A、[-4,4] |
| B、[-3,0)∪(0,3]∪{-4,4} |
| C、[-3,3]∪{-4,4} |
| D、(-4,4) |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据函数的奇偶性求出函数f(x)的表达式,然后根据函数的图象利用数形结合即可得到结论.
解答:
解:∵f(x)是定义在R上的奇函数,
∴f(0)=0,
若x<0,则-x>0,
∵x>0时,f(x)=x2-2x-3,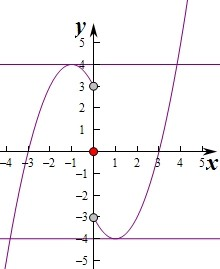
∴f(-x)=x2+2x-3=-f(x),
∴x<0时,f(x)=-x2-2x+3,
则f(x)=
,
作出函数f(x)的图象如图:
要使f(x)=a有两个根,
则a=4或a=-4,0<a≤3或-3≤a<0,
即实数a的取值范围是[-3,0)∪(0,3]∪{-4,4},
故选:B.
∴f(0)=0,
若x<0,则-x>0,
∵x>0时,f(x)=x2-2x-3,

∴f(-x)=x2+2x-3=-f(x),
∴x<0时,f(x)=-x2-2x+3,
则f(x)=
|
作出函数f(x)的图象如图:
要使f(x)=a有两个根,
则a=4或a=-4,0<a≤3或-3≤a<0,
即实数a的取值范围是[-3,0)∪(0,3]∪{-4,4},
故选:B.
点评:本题主要考查函数奇偶性的应用,根据函数的奇偶性求出函数的表达式是解决本题的关键,利用数形结合是解决本题的基本数学思想.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
已知直线ax+by+1=0中的a,b是取自集合{-3,-2,-1,0,1,2}中的2个不同的元素,并且直线的倾斜角大于60°,那么符合这些条件的直线共有( )
| A、16条 | B、13条 |
| C、11条 | D、8条 |
集合A={0,1,2,3,4},B={x|x2-x>0},则A∩B=( )
| A、{2,3,4} |
| B、{1} |
| C、{x|2<x≤4} |
| D、{x|x<0或x>2} |
已知函数f(x)=ln(ex-1)(x>0)( )
| A、若f(a)+2a=f(b)+3b,则a>b |
| B、若f(a)+2a=f(b)+3b,则a<b |
| C、若f(a)-2a=f(b)-3b,则a>b |
| D、若f(a)-2a=f(b)-3b,则a<b |