题目内容
德阳中学数学竞赛培训共开设有初等代数、初等几何、初等数论和微积分初步共四门课程,要求初等代数、初等几何都要合格,且初等数论和微积分初步至少有一门合格,则能取得参加数学竞赛复赛的资格,现有甲、乙、丙三位同学报名参加数学竞赛培训,每一位同学对这四门课程考试是否合格相互独立,其合格的概率均相同,(见下表),且每一门课程是否合格相互独立,
(1)求甲同学取得参加数学竞赛复赛的资格的概率;
(2)记ξ表示三位同学中取得参加数学竞赛复赛的资格的人数,求ξ的分布列及期望Eξ.
| 课 程 | 初等代数 | 初等几何 | 初等数论 | 微积分初步 | ||||||||
| 合格的概率 |
|
|
|
|
(2)记ξ表示三位同学中取得参加数学竞赛复赛的资格的人数,求ξ的分布列及期望Eξ.
考点:二项分布与n次独立重复试验的模型,古典概型及其概率计算公式,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)分别记甲对这四门课程考试合格为事件A,B,C,D,“甲能能取得参加数学竞赛复赛的资格”的概率为P(ABCD)+P(ABC
)+P(AB
D),由事件A,B,C,D相互独立能求出结果.
(2)由题设知ξ的所有可能取值为0,1,2,3,ξ~B(3,
),由此能求出ξ的分布列和数学期望.
. |
| D |
. |
| C |
(2)由题设知ξ的所有可能取值为0,1,2,3,ξ~B(3,
| 5 |
| 12 |
解答:
解:(1)分别记甲对这四门课程考试合格为事件A,B,C,D,
且事件A,B,C,D相互独立,
“甲能能取得参加数学竞赛复赛的资格”的概率为:
P(ABCD)+P(ABC
)+P(AB
D)
=
•
•
•
+
•
•
•
+
•
•
•
=
.
(2)由题设知ξ的所有可能取值为0,1,2,3,ξ~B(3,
),
P(ξ=0)=
(
)3=
,
P(ξ=1)=
(
)(
)2=
,
P(ξ=2)=
(
)2(
)=
,
P(ξ=3)=
(
)3=
,
∴ξ的分布列为:
∵ξ~B(3,
),
∴Eξ=3×
=
.
且事件A,B,C,D相互独立,
“甲能能取得参加数学竞赛复赛的资格”的概率为:
P(ABCD)+P(ABC
. |
| D |
. |
| C |
=
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
(2)由题设知ξ的所有可能取值为0,1,2,3,ξ~B(3,
| 5 |
| 12 |
P(ξ=0)=
| C | 0 3 |
| 7 |
| 12 |
| 343 |
| 1728 |
P(ξ=1)=
| C | 1 3 |
| 5 |
| 12 |
| 7 |
| 12 |
| 735 |
| 1728 |
P(ξ=2)=
| C | 2 3 |
| 5 |
| 12 |
| 7 |
| 12 |
| 525 |
| 1728 |
P(ξ=3)=
| C | 3 3 |
| 5 |
| 12 |
| 125 |
| 1728 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 12 |
∴Eξ=3×
| 5 |
| 12 |
| 5 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是历年高考的必考题型之一,是中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知函数f(x)=ln(ex-1)(x>0)( )
| A、若f(a)+2a=f(b)+3b,则a>b |
| B、若f(a)+2a=f(b)+3b,则a<b |
| C、若f(a)-2a=f(b)-3b,则a>b |
| D、若f(a)-2a=f(b)-3b,则a<b |
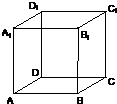 电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.
电子蛙跳游戏是:青蛙第一步从如图所示的正方体ABCD-A1B1C1D1顶点A起跳,每步从一顶点跳到相邻的顶点.