题目内容
已知椭圆
+
=1(a>b>0)经过点M(
,1),离心率为
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知点P(
,0),若A,B为已知椭圆上两动点,且满足
•
=-2,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| ||
| 2 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知点P(
| 6 |
| PA |
| PB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
=
,
+
=1,又a2=b2+c2,由此能求出椭圆方程.
(Ⅱ)当直线AB与x轴不垂直时,设直线AB方程为y=kx+m,代入
+
=1,消去y整理,得(2k2+1)x2+4kmx+2m2-8=0,由根的判别式和韦达定理结合已知条件求出直线AB的方程为y=k(x-
),从而得到直线AB经过定点(
,0).当直线AB与x轴垂直时,直线方程为x=
,也有
•
=-2.由此证明直线AB一定过定点(
,0).
| c |
| a |
| ||
| 2 |
| 6 |
| a2 |
| 1 |
| b2 |
(Ⅱ)当直线AB与x轴不垂直时,设直线AB方程为y=kx+m,代入
| x2 |
| 8 |
| y2 |
| 4 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| PA |
| PB |
2
| ||
| 3 |
解答:
解:(Ⅰ)∵椭圆
+
=1(a>b>0)离心率为
,∴
=
,①
∵椭圆经过点M(
,1),∴
+
=1,②
又a2=b2+c2,③
∴由①②③联立方程组解得a2=8,b2=c2=4,
∴椭圆方程为
+
=1.
(Ⅱ)①当直线AB与x轴不垂直时,设直线AB方程为y=kx+m,
代入
+
=1,消去y整理,得(2k2+1)x2+4kmx+2m2-8=0,
由△>0,得8k2+4-m2>0,(*)
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
,
∵点P(
,0),A,B为已知椭圆上两动点,且满足
•
=-2,
∴
•
=(x1-
)(x2-
)+y1y2
=(x1-
)(x2-
)+(kx1+m)(kx2+m)
=(k2+1)x1x2+(km-
)(x1+x2)+6+m2=-2,
∴(k2+1)•
+(km-
)•
+8+m2=0,
整理,得(
m+2
k)2=0,
解得m=-
k,满足(*)
∴直线AB的方程为y=k(x-
),
∴直线AB经过定点(
,0).
②当直线AB与x轴垂直时,直线方程为x=
,
此时A(
,
),B(
,-
),也有
•
=-2,
综上,直线AB一定过定点(
,0).
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| c |
| a |
| ||
| 2 |
∵椭圆经过点M(
| 6 |
| 6 |
| a2 |
| 1 |
| b2 |
又a2=b2+c2,③
∴由①②③联立方程组解得a2=8,b2=c2=4,
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
(Ⅱ)①当直线AB与x轴不垂直时,设直线AB方程为y=kx+m,
代入
| x2 |
| 8 |
| y2 |
| 4 |
由△>0,得8k2+4-m2>0,(*)
设A(x1,y1),B(x2,y2),则x1+x2=-
| 4km |
| 2k2+1 |
| 2m2-8 |
| 2k2+1 |
∵点P(
| 6 |
| PA |
| PB |
∴
| PA |
| PB |
| 6 |
| 6 |
=(x1-
| 6 |
| 6 |
=(k2+1)x1x2+(km-
| 6 |
∴(k2+1)•
| 2m2-8 |
| 2k2+1 |
| 6 |
| -4km |
| 2k2+1 |
整理,得(
| 3 |
| 2 |
解得m=-
2
| ||
| 3 |
∴直线AB的方程为y=k(x-
2
| ||
| 3 |
∴直线AB经过定点(
2
| ||
| 3 |
②当直线AB与x轴垂直时,直线方程为x=
2
| ||
| 3 |
此时A(
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| PA |
| PB |
综上,直线AB一定过定点(
2
| ||
| 3 |
点评:本题考查椭圆方程的求法,考查直线是否过定点的判断与证明,综合性强,难度大,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
育英学校派出5名优秀教师去边远地区的三所中学进行教学交流,每所中学至少派一名教师,则不同的分配方法有( )
| A、80种 | B、90种 |
| C、120种 | D、150种 |
长方体ABCD-A1B1C1D1,AB=2,AD=2,AA1=
,则点D到平面ACD1的距离是( )
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
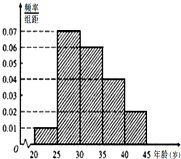 近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召N名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.
近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召N名义务宣传志愿者,成立环境保护宣传组织.现把该组织的成员按年龄分成5组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示,已知第2组有35人.