题目内容
（1）已知|x-4|+|3-x|＜a若不等式的解集为空集，求a的范围
（2）已知a，b，c∈R+，且a+b+c=1，求证：a2+b2+c2≥
．
（2）已知a，b，c∈R+，且a+b+c=1，求证：a2+b2+c2≥
| 1 |
| 3 |
考点：不等式的证明
专题：不等式的解法及应用
分析：（1）利用绝对值三角不等式求出左侧部分的最小值，然后转化求出a的范围．
（2）利用已知条件求出1的平方，利用重要不等式求出结果即可．
（2）利用已知条件求出1的平方，利用重要不等式求出结果即可．
解答：
（1）解：∵|x-4|+|3-x|≥|（x-4）+（3-x）|=1，
又|x-4|+|3-x|＜a若不等式的解集为空集，
∴a≤1…（5分）
（2）证明：由a+b+c=1，得1=（a+b+c）2=a2+b2+c2+2ab+2bc+2ac≤3（a2+b2+c2）
∴a2+b2+c2≥
．（当且仅当a=b=c时取等号） …（10分）
又|x-4|+|3-x|＜a若不等式的解集为空集，
∴a≤1…（5分）
（2）证明：由a+b+c=1，得1=（a+b+c）2=a2+b2+c2+2ab+2bc+2ac≤3（a2+b2+c2）
∴a2+b2+c2≥
| 1 |
| 3 |
点评：本题考查绝对值不等式的解法，不等式的证明，考查分析问题解决问题的能力．
练习册系列答案
相关题目
设m、n是两条不同的直线，α、β是两个不同的平面．下列四个命题中，正确的是（ ）
| A、α∥β，m?α，n?β，则m∥n |
| B、α⊥β，m⊥β，则m∥α或m?α |
| C、α⊥β，m?α，n?β，则m⊥n |
| D、α∥β，m⊥β，n⊥α，则m∥n |
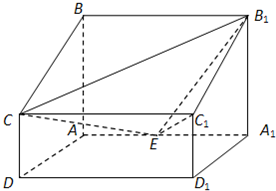四棱柱ABCD-A1B1C1D1中，AA1⊥底面ABCD，AB∥CD，AB⊥AD，AD=CD=1，AA1=AB=2，E为AA1的中点．
正三棱锥P-ABC的高为2，侧棱与底面所成的角为45°，则点A到侧面PBC的距离是（ ）
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|